题目内容
如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD于点O,∠BAC=60°,若BC= ,则此梯形的面积为
,则此梯形的面积为

 ,则此梯形的面积为
,则此梯形的面积为| A.2 | B. | C. | D. |

D
分析:过O作EF⊥AD交AD于E,交BC于F,根据等腰梯形的性质得出∠ABC=∠DCB,证△ABC≌△DCB,推出∠DBC=∠ACB,求出∠DBC=∠ACB=45°,根据直角三角形性质求出OF,根据勾股定理求出OB、OA,OE、AD,根据面积公式即可求出面积.
解答: 解:过O作EF⊥AD交AD于E,交BC于F,
解:过O作EF⊥AD交AD于E,交BC于F,
∵等腰梯形ABCD,AD∥BC,AB=CD,
∴∠ABC=∠DCB,
∵BC=BC,
∴△ABC≌△DCB,
∴∠DBC=∠ACB,
∵AC⊥BD,
∴∠BOC=90°,
∴∠DBC=∠ACB=45°,
∴OB=OC,
∵OF⊥BC,
∴OF=BF=CF= BC=
BC= ,
,
由勾股定理得:OB= ,
,
∵∠BAC=60°,
∴∠ABO=30°,
∴AB=2OA,
由勾股定理得:(2OA)2=OA2+( )2,
)2,
∴OA=1,AB=2,
同法可求OD=OA=1,AD= ,OE=
,OE= ,
,
S梯形ABCD= (AD+BC)?EF=
(AD+BC)?EF= ×(
×( +
+ )×(
)×( +
+ )=2+
)=2+ .
.
故答案为:D
解答:
 解:过O作EF⊥AD交AD于E,交BC于F,
解:过O作EF⊥AD交AD于E,交BC于F,∵等腰梯形ABCD,AD∥BC,AB=CD,
∴∠ABC=∠DCB,
∵BC=BC,
∴△ABC≌△DCB,
∴∠DBC=∠ACB,
∵AC⊥BD,
∴∠BOC=90°,
∴∠DBC=∠ACB=45°,
∴OB=OC,
∵OF⊥BC,
∴OF=BF=CF=
 BC=
BC= ,
,由勾股定理得:OB=
 ,
,∵∠BAC=60°,
∴∠ABO=30°,
∴AB=2OA,
由勾股定理得:(2OA)2=OA2+(
 )2,
)2,∴OA=1,AB=2,
同法可求OD=OA=1,AD=
 ,OE=
,OE= ,
,S梯形ABCD=
 (AD+BC)?EF=
(AD+BC)?EF= ×(
×( +
+ )×(
)×( +
+ )=2+
)=2+ .
.故答案为:D

练习册系列答案
相关题目



 (B)5
(B)5 (C)5 (D)10
(C)5 (D)10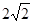 ,CD=
,CD= ,
, ,则点P的个数为【 】
,则点P的个数为【 】
 珠海)(本题满分6分)如图,在正方形ABC1D1中,AB=1.连接AC1,
珠海)(本题满分6分)如图,在正方形ABC1D1中,AB=1.连接AC1,

 中,
中, ,
, ,
, ,在
,在 上截取
上截取 ,使
,使 ,过点
,过点 作
作 于
于 于点
于点 ,连接
,连接 ,交
,交 于点
于点 ,交
,交
 。
。

 ,
, ,求
,求