题目内容
13.二次函数y=ax2+bx+c(a≠0)的图象过(1,0),(2,0),且最大值为$\frac{1}{2}$,求二次函数的解析式.分析 根据题意求得顶点坐标($\frac{3}{2}$,$\frac{1}{2}$),设出顶点式y=a(x+$\frac{3}{2}$)2+$\frac{1}{2}$,然后代入(1,0),从而求得a的值,即得这个二次函数的解析式.
解答 解:∵二次函数y=ax2+bx+c的图象经过点(1,0),(2,0),
∴对称轴为:x=$\frac{3}{2}$,
∴顶点坐标为:($\frac{3}{2}$,$\frac{1}{2}$),
设此二次函数解析式为:y=a(x+$\frac{3}{2}$)2+$\frac{1}{2}$,
∴0=a(1+$\frac{3}{2}$)2+$\frac{1}{2}$,
解得:a=-$\frac{1}{5}$,
∴这个二次函数的解析式为y=-$\frac{1}{5}$(x+$\frac{3}{2}$)2+$\frac{1}{2}$.
点评 本题考查了用待定系数法求函数解析式的方法,同时还考查了方程组的解法等知识,难度不大.

练习册系列答案
相关题目
3.下列等式成立的是( )
| A. | $\sqrt{7}$-$\sqrt{2}$=$\sqrt{5}$ | B. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | C. | $\sqrt{{2}^{2}+{3}^{2}}$=5 | D. | -$\sqrt{(-5)^{2}}$=5 |
 如图,在一块长AB=a cm,宽BC=b cm的长方形草地上,有三条宽都是2m的小路,则这块草地的绿地面积为(a-4)(b-2)cm2.
如图,在一块长AB=a cm,宽BC=b cm的长方形草地上,有三条宽都是2m的小路,则这块草地的绿地面积为(a-4)(b-2)cm2.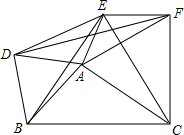 如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF,且∠BAC≠60°.
如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF,且∠BAC≠60°.