题目内容
如图1, 在直角梯形ABCD中,![]() ,
,![]() 90°,
90°,![]() ,
,![]() .点
.点![]() 从点D出发以每秒2个单位长度的速度向点
从点D出发以每秒2个单位长度的速度向点![]() 运动,同时,点
运动,同时,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度向点
出发,以每秒1个单位长度的速度向点![]() 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点![]() 作
作![]() 于点
于点![]() ,连结AC交NP于点Q,连结MQ.
,连结AC交NP于点Q,连结MQ.
设运动时间为t秒.
(1)填空:AM= ,AP= .(用含t的代数式表示)
(2)t取何值时,梯形ABNM面积等于梯形ABCD面积的一半;
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻![]() ,使四边形AQMK 为正方形?并说明理由.
,使四边形AQMK 为正方形?并说明理由.

解:(1)AM=4-2t ………………2分
AP=1+t ………………4分
(2)∵梯形ABNM面积等于梯形ABCD面积的一半
∴![]() ………………6分
………………6分
解得 ![]() ………………8分
………………8分
∴当![]() 时,梯形ABNM面积等于梯形ABCD面积的一半 ………9分
时,梯形ABNM面积等于梯形ABCD面积的一半 ………9分
(3) 存在
∵ ![]() ,
,![]()
∴ ![]()
∵ △AQM沿AD翻折,得△AKM
∴ QM=MK, AQ=AK
∠KAQ=2∠CAD=90° ………………11分
要使四边形AQMK为正方形
则 AQ=MQ ………………12分
∵![]() ∴
∴![]() ∴
∴![]() ∴
∴![]() ∴
∴![]()
![]()
∴ 当![]() 时,四边形AQMK为正方形 ………………14分
时,四边形AQMK为正方形 ………………14分


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
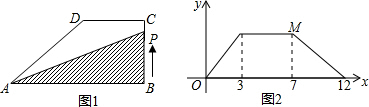
假期作业暑假成长乐园新疆青少年出版社系列答案 如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )
如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )| A、3 | B、4 | C、5 | D、6 |