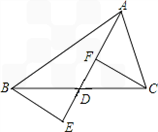
题目内容
如图，已知，D是BC的中点，E是AD的中点，则AF：FC=________．
1：2
分析：过点D作DM∥AC，根据中位线定理及△BDM∽△BCF可知，FC=2DM，再根据△DEM∽△AEF即可解答．
解答：
解：过点D作DM∥AC，交BF于M，则△BDM∽△BCF，△DEM∽△AEF，
由△BDM∽△BCF，D是BC的中点，E是AD的中点可知，
，
则FC=2DM
根据△DEM∽△AEF得到AF=DM，因而AF：FC=DM：2DM=1：2．
点评：本题主要考查了相似性的性质，利用作平行线从而作出相似的三角形，把两个线段的比进行转化．
分析：过点D作DM∥AC，根据中位线定理及△BDM∽△BCF可知，FC=2DM，再根据△DEM∽△AEF即可解答．
解答：
解：过点D作DM∥AC，交BF于M，则△BDM∽△BCF，△DEM∽△AEF，由△BDM∽△BCF，D是BC的中点，E是AD的中点可知，
，则FC=2DM
根据△DEM∽△AEF得到AF=DM，因而AF：FC=DM：2DM=1：2．
点评：本题主要考查了相似性的性质，利用作平行线从而作出相似的三角形，把两个线段的比进行转化．
练习册系列答案
计算高手系列答案
相关题目
20、如图，已知：AD是BC上的中线，且DF=DE．求证：BE∥CF．
如图，已知，D是BC的中点，E是AD的中点，则AF：FC=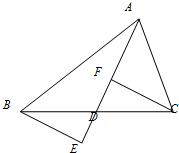
23、如图，已知：AD是BC上的中线，E点在AD延长线上，且DF=DE．
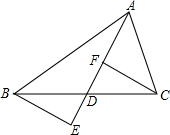如图，已知：AD是BC上的中线，BE⊥AD于点E，且DF=DE．求证：CF⊥AD．