Question

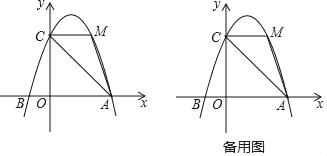
【题目】如图，已知抛物线过点A（3，0），B（﹣1，0），C（0，3），连接AC，点M是抛物线AC段上的一点，且CM∥x轴．

（1）求抛物线的解析式；

（2）求∠CAM的正切值；

（3）点Q在抛物线上，且∠BAQ=∠CAM，求点Q的坐标．

Answer 1

【答案】（1）y=﹣x2+2x+3；（2）tan∠CAM=；（3）Q的坐标为（﹣，）或（﹣，﹣）．

【解析】

设抛物线的解析式为y=a（x﹣3）（x+1），将点C的坐标代入的a即可求得抛物线的解析式.

作MD⊥AC于D，证明是等腰直角三角形又CM∥x轴，所以∠ACM=45°，是等腰直角三角形求得DM，再根据勾股定理求得AD，即可求得结果.

设点Q（x，﹣x2+2x+3），根据∠BAQ=∠CAM且tan∠CAM=列出解出x的两个解，代入Q（x，﹣x2+2x+3）即可求解.

（1）设抛物线的解析式为y=a（x﹣3）（x+1），将点C的坐标代入得：﹣3a=3，解得：a=﹣1，

∴抛物线的解析式为y=﹣x2+2x+3．

（2）作MD⊥AC于D，是

∵CM∥AB，由抛物线y=﹣x2+2x+3可知M点的坐标为（2，3），

∵C（0，3），A（3，0）

∴AO=OC=3，

∵∠MDC=90°

∴∠OAC=∠ACO=45°，

∴∠ACM=45°，

∴CD=DM，

∵CM=2，

∴DM=CM=，

∴CD=，

∵AC2=OA2+OC2

∴AC=3．

∴AD=AC﹣CD=2，

∴tan∠CAM===；

③设点Q（x，﹣x2+2x+3）．

∵∠BAQ=∠CAM且tan∠CAM=，

∴=±，整理得：x+1=±，解得：x=﹣或x=﹣．

当x=﹣时，y=，

∴Q（﹣，）．

当x=﹣时，y=﹣．

∴Q（﹣，﹣）．

综上所述，点Q的坐标为（﹣，）或（﹣，﹣）．