题目内容
如图，D为⊙O直径AB延长线上一点，PD是⊙O的切线，∠D＝30°．
求证：PA＝PD．
答案：
解析：
提示：
解析：
|
证明：连接OP．
∵PD是⊙O的切线，P为切点， ∴OP⊥PD(圆的切线垂直于过切点的半径) 在Rt△OPD中，∵∠D＝30°， ∴∠POD＝60°． ∵OA＝OP，∴∠A＝∠OPA． ∵∠POD＝∠A＋∠OPA＝2∠A， ∴∠A＝30°． ∴∠A＝∠D．∴PA＝PD． |
提示：
|
如图，欲判定⊙C与直线AB的关系，只需先求出圆心C到直线AB的距离CD的长，然后再与r比较即可． |
练习册系列答案
阅读快车系列答案
相关题目
6、如图，AB为直径，∠BED=40°，则∠ACD=（ ）
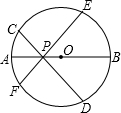
如图，AB为⊙O直径，CE切⊙O于点C，CD⊥AB，D为垂足，AB=12cm，∠B=30°，则∠ECB=
如图，AB为直径，∠BED=40°，则∠ACD=
如图，AB为⊙O直径，D为