题目内容
11. 如图,AB是⊙O的直径,弦CD⊥AB于点H,⊙O的切线EF与AC平行,且与CD的延长线交于点E,与AB的延长线交于点F,切点为G,连接AG交CD于K.
如图,AB是⊙O的直径,弦CD⊥AB于点H,⊙O的切线EF与AC平行,且与CD的延长线交于点E,与AB的延长线交于点F,切点为G,连接AG交CD于K.(1)求证:KE=GE;
(2)求证:KG2=KD•GE.
分析 (1)如图1,连接OG.根据切线性质及CD⊥AB,可以推出连接∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE;
(2)如图2,连接GD.利用平行线的性质和圆周角定理得到∠KGD=∠E.又由(1)知∠KGE=∠GKE,则△GKD∽△EGK,所以由相似三角形的对应边成比例得到关于KG的比例式,由比例式的基本性质即可得到KG2=KD•GE.
解答 解:(1)如图1,连接OG.
∵EG为切线,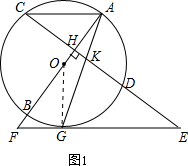
∴∠KGE+∠OGA=90°.
∵CD⊥AB,
∴∠AKH+∠OAG=90°,
又∵OA=OG,
∴∠OGA=∠OAG,
∴∠KGE=∠AKH=∠GKE,
∴KE=GE;
(2)证明:如图2,连接GD.
∵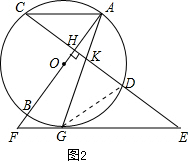 AC∥EF,
AC∥EF,
∴∠C=∠E.
又∵∠C=∠AGD,
∴∠KGD=∠E.
又∵由(1)知∠KGE=∠GKE,
∴△GKD∽△EGK,
∴$\frac{KG}{GE}=\frac{KD}{KG}$,
即KG2=KD•GE.
点评 此题考查了切线的性质,相似三角形的判定与性质,垂径定理,圆周角定理,平行线的判定,以及等腰三角形的判定和性质,熟练掌握各种几何图形定理及性质是解本题的关键.

练习册系列答案
相关题目
2.下列式子是分式的是( )
| A. | $\frac{a}{4}$ | B. | $\frac{1}{2}{x}^{2}$ | C. | $\frac{x}{π}$ | D. | $\frac{1}{a}$ |
19.已知$\frac{a}{b}=\frac{c}{d}=\frac{2}{3}$(b+d≠0),则$\frac{a+c}{b+d}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
6. 如图,圆上有A,B,C,D四点,其中∠BAD=80°,若圆的半径为9,则$\widehat{BAD}$的长度为( )
如图,圆上有A,B,C,D四点,其中∠BAD=80°,若圆的半径为9,则$\widehat{BAD}$的长度为( )
 如图,圆上有A,B,C,D四点,其中∠BAD=80°,若圆的半径为9,则$\widehat{BAD}$的长度为( )
如图,圆上有A,B,C,D四点,其中∠BAD=80°,若圆的半径为9,则$\widehat{BAD}$的长度为( )| A. | 4π | B. | 8π | C. | 10π | D. | 15π |
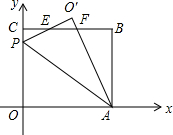 在平面直角坐标系中,O是坐标原点,矩OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8),点P是y轴上的一个动点,将△OAP沿AP翻折得到:△O′AP,直线BC与直线O′P交于点E,与直线O′A交于点F.
在平面直角坐标系中,O是坐标原点,矩OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8),点P是y轴上的一个动点,将△OAP沿AP翻折得到:△O′AP,直线BC与直线O′P交于点E,与直线O′A交于点F. 二次函数y=ax2+bx+c的图象如图所示,其对称轴与x轴交于点(-1,0),图象上有三个点分别为(2,y1),(-3,y2),(0,y3),则y1、y2、y3的大小关系是y3<y2<y1(用“>”“<”或“=”连接).
二次函数y=ax2+bx+c的图象如图所示,其对称轴与x轴交于点(-1,0),图象上有三个点分别为(2,y1),(-3,y2),(0,y3),则y1、y2、y3的大小关系是y3<y2<y1(用“>”“<”或“=”连接). 如图,在△ABC中,点D,E分别在边AB和AC上,已知DE∥BC,∠DBE=32°,∠EBC=26°,则∠BDE的度数是122°.
如图,在△ABC中,点D,E分别在边AB和AC上,已知DE∥BC,∠DBE=32°,∠EBC=26°,则∠BDE的度数是122°.