Question

1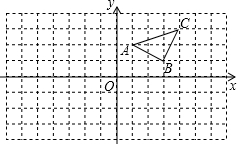．已知：如图所示．
（1）作出△ABC关于y轴对称的△A′B′C′，并写出△A′B′C′三个顶点的坐标．
（2）在x轴上画出点P，使PA+PC最小，并直接写出此时PA+PC的最小值．

Answer 1

分析 （1）分别作出A、B、C三点关于y轴的对称点A′、B′、C′即可．
（2）作点C关于x轴的对称点C″，连接AC″交x轴于P，此时PA+PC最短．PA+PC的最小值=PC″．

解答 解：（1）△ABC关于y轴对称的△A′B′C′如图所示．

A′（-1，2），B′（-3，1），C′（-4，3）．

（2）作点C关于x轴的对称点C″，连接AC″交x轴于P，此时PA+PC最短．
∵A（1，2），C″（4，-3），
∴PA+PC的最小值=PA+PC″=AC″=$\sqrt{（1-4）^{2}+（2+3）^{2}}$=$\sqrt{34}$．

点评 本题考查作图-轴对称变换，轴对称-最短问题，两点之间线段最短等知识，解题的关键是熟练掌握轴对称的概念，学会利用对称解决最短问题，属于中考常考题型．