题目内容
11. 如图,△ABC是⊙O的内接三角形,AD平分∠BAC交圆于点D,CE平分∠ACB交AD于点E,连接BD,求证:BD=ED.
如图,△ABC是⊙O的内接三角形,AD平分∠BAC交圆于点D,CE平分∠ACB交AD于点E,连接BD,求证:BD=ED.
分析 连接CD,由AD平分∠BAC交⊙O于D得∠1=∠2,根据圆周角定理得$\widehat{BD}$=$\widehat{CD}$,则BD=CD,再利用CE平分∠ACB交AD于点E,可得∠3=∠4,然后证明∠CED=∠DCE,根据等腰三角形的判定得到CD=ED,即BD=ED.
解答 证明:连接CD,如图所示,
∵AD平分∠BAC交⊙O于D,
∴∠1=∠2,
∴得$\widehat{BD}$=$\widehat{CD}$,
∴BD=CD,
∵CE平分∠ACB交AD于点E,
∴∠3=∠4,
∵∠CED=∠2+∠3,
∵∠1=∠5,
∴∠DCE=∠4+∠5=∠1+∠4=∠2+∠3,
即∠CED=∠DCE,
∴CD=ED,
即BD=ED.
点评 此题考查了圆周角定理,三角形的角平分线的定义,三角形外角的性质及等腰三角形的判定,解题的关键是:添加辅助线,体现转化的思想.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
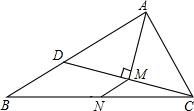 如图,在△ABC中,AB=5,AC=3,点N为BC的中点,AM平分∠BAC,CM⊥AM,垂足为点M,延长CM交AB于点D,求MN的长.
如图,在△ABC中,AB=5,AC=3,点N为BC的中点,AM平分∠BAC,CM⊥AM,垂足为点M,延长CM交AB于点D,求MN的长.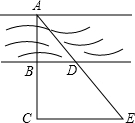 如图,为了测量河宽,小华采用的办法是:在河的对岸选取一点A,在河的这岸选一点B,使AB与河的边缘垂直,然后在AB的延长线上取一点C,并量得BC=30米;在河的这边取一点D,并量得BD=20米;最后在射线AD上取一点E,使得CE∥BD,并量得DE=40米.小华这种做法,她能根据已有的数据求出河宽AB吗?若能,请求出河宽AB;若不能,她还必须测量哪一条线段的长?假设这条线段的长是m米,请你用含m的代数式表示河宽AB.
如图,为了测量河宽,小华采用的办法是:在河的对岸选取一点A,在河的这岸选一点B,使AB与河的边缘垂直,然后在AB的延长线上取一点C,并量得BC=30米;在河的这边取一点D,并量得BD=20米;最后在射线AD上取一点E,使得CE∥BD,并量得DE=40米.小华这种做法,她能根据已有的数据求出河宽AB吗?若能,请求出河宽AB;若不能,她还必须测量哪一条线段的长?假设这条线段的长是m米,请你用含m的代数式表示河宽AB.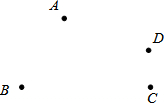 如图,A、B、C、D四点不在同一直线上,读句画图.
如图,A、B、C、D四点不在同一直线上,读句画图.