题目内容
13. 如图,在△ABC中,∠BAC=50°,AD为∠BAC的平分线,DE⊥AB,DF⊥AC,则∠DEF=25度.
如图,在△ABC中,∠BAC=50°,AD为∠BAC的平分线,DE⊥AB,DF⊥AC,则∠DEF=25度.
分析 根据垂直的定义、四边形内角和定理求出∠EDF,根据角平分线的性质得到DE=DF,根据等腰三角形的性质、三角形内角和定理计算即可.
解答 解:∵∠BAC=50°,DE⊥AB,DF⊥AC,
∴∠EDF=130°,
∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∴∠DEF=∠DFE=25°,
故答案为:25.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
4.已知|a|=3,那么a=( )
| A. | 3 | B. | -3 | C. | ±3 | D. | 不存在 |
5.下列四个图形中,线段AD是△ABC的高的是( )
| A. |  | B. |  | C. |  | D. |  |
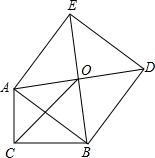 如图,Rt△ABC中,C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点D,连接OC,已知AC=5,OC=6,则另一直角边BC的长为6$\sqrt{2}$-5.
如图,Rt△ABC中,C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点D,连接OC,已知AC=5,OC=6,则另一直角边BC的长为6$\sqrt{2}$-5. 如图,△DEF是由△ABC平移而得到的,并且BC=11,EC=6,AB=15,则CF的长为( )
如图,△DEF是由△ABC平移而得到的,并且BC=11,EC=6,AB=15,则CF的长为( )