题目内容
(本小题8分)
(1)解方程 ;
;
(2)利用判别式判断方程 的根的情况.
的根的情况.
(1) =1;
=1; =-3;(2)方程有两个不相等的实数根.
=-3;(2)方程有两个不相等的实数根.
【解析】
试题分析:(1)利用因式分解的法则求出方程的解;(2)首先求出△的值,然后根据△的值判定根的情况.
试题解析:(1)原方程可化为: +2x-3=0 (x-1)(x+3)=0
+2x-3=0 (x-1)(x+3)=0
解得: =1
=1  =-3
=-3
(2)a=2 b=-3 c=- 则△=
则△= -4ac=9-4×2×(-
-4ac=9-4×2×(- )=9+12=21>0
)=9+12=21>0
∴方程有两个不相等的实数根.
考点:一元二次方程的解法;根的判别式.
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 ,其中
,其中 .
.
 和
和 重合放置,其中
重合放置,其中 90°,
90°, 30°,
30°, .
.
 ,将△
,将△ 绕点
绕点 旋转,当点
旋转,当点 恰好落在
恰好落在 边上时,m]
边上时,m] = °,旋转角α= °(0<α<90),线段
= °,旋转角α= °(0<α<90),线段 与
与 的位置关系是 ;
的位置关系是 ; 的面积为
的面积为 ,△
,△ 的面积为
的面积为 ,则
,则 与
与 的数量关系是 ;
的数量关系是 ; ,
, 边上的高
边上的高 ,
, ,请你证明小明的猜想;
,请你证明小明的猜想;
 60°,
60°, 平分
平分 ,
, ,
, ∥
∥ 交
交 于点
于点 .若在射线
.若在射线 上存在点
上存在点 ,使
,使 ,请直接写出相应的
,请直接写出相应的 的长.
的长.
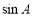 =( )
=( )
 (B)
(B)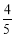 (C)
(C) (D)
(D)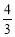

 B.
B. C.
C. D.
D.