��Ŀ����
����С��10�֣�
��ͼ�٣���������ȫ��ͬ��������ֽƬ ��
�� �غϷ��ã�����
�غϷ��ã����� 90�㣬
90�㣬 30�㣬
30�㣬 ��
��

��1����������
��ͼ�ڣ��̶��� ������
������ �Ƶ�
�Ƶ� ��ת������
��ת������ ǡ������
ǡ������ ����ʱ��m]
����ʱ��m]
�� = �㣬��ת�Ǧ�= �㣨0������90�����߶�
= �㣬��ת�Ǧ�= �㣨0������90�����߶� ��
�� ��λ�ù�ϵ�� ��
��λ�ù�ϵ�� ��
����� �����Ϊ
�����Ϊ ����
���� �����Ϊ
�����Ϊ ����
���� ��
�� ��������ϵ�� ��
��������ϵ�� ��
��2��������֤
���� �Ƶ�
�Ƶ� ��ת��ͼ����ʾ��λ��ʱ��С�����루����
��ת��ͼ����ʾ��λ��ʱ��С�����루���� ��
�� ��������ϵ��Ȼ�����������Էֱ������ˡ�
��������ϵ��Ȼ�����������Էֱ������ˡ� �͡�
�͡� ��
�� ��
�� ���ϵĸ�
���ϵĸ� ��
�� ������֤��С���IJ��룻
������֤��С���IJ��룻

��3����չ̽��
��ͼ�ܣ� 60�㣬
60�㣬 ƽ��
ƽ�� ��
�� ��
�� ��
�� ��
�� �ڵ�
�ڵ� ����������
���������� �ϴ��ڵ�
�ϴ��ڵ� ��ʹ
��ʹ ����ֱ��д����Ӧ��
����ֱ��д����Ӧ�� �ij���
�ij���

��1����60�� 60�� ��
�� �� ��
�� �� �� ��2������������3��
�� ��2������������3�� ��
�� ��
��
��������
�����������1��������ת�õ��Լ�ֱ���������нǶȵĹ�ϵ�ó��ȱ������Σ�����Ƕ��Լ��߶�֮��Ĺ�ϵ����2������������ȫ�ȵó������ε������ϵ����3���� ��ON��OM�ڵ�
��ON��OM�ڵ� ����
���� ��OM�ڵ�
��OM�ڵ� ��
�� ��
�� ������.
������.
�����������1����60 60  ��
�� ��
�� ��
��
��2��֤���ߡ� �ɡ�
�ɡ� ��ת�õ������
��ת�õ������ �ա�
�ա� ����
���� 90�㣮
90�㣮
�� 360�㣬��
360�㣬�� 180�㣮��
180�㣮�� 180�㣬
180�㣬
�� ����
���� 90�㣬
90�㣬 �����
����� �ա�
�ա� ��
��
�� �� ��
�� �� ��
�� ��
�� ����
���� ��
��
��3�� ��
�� ��
��
���㣺������ȫ�ȵ�֤��������.
��������� ����1�������� ��1�������εĸ���ɲ���ͬһ��ֱ���ϵ������߶���β˳���������ɵ�ͼ�ν��������Σ���������ε��߶ν��������εıߣ�
�������ߵĹ����˵���������εĶ��㣮
����������ɵĽǽ��������ε��ڽǣ���������εĽǣ�
��2�����ߵ���ȹ�ϵ���ࣺ���ȱ������κ͵��������Σ��������ȵĵ��������Ρ�������ȵĵ��������μ��ȱ������Σ���
��3�������ε���Ҫ�߶Σ���ƽ���ߡ����ߡ��ߣ�
��4�������ξ����ȶ��ԣ� ����2��ͼ�ε�ƽ������ת ���壺
��һ��ͼ����ij�������ƶ�һ���ľ��룬������ͼ���˶���Ϊƽ�ơ�ƽ����ͼ�α任��һ�ֻ�����ʽ��ƽ�Ʋ��ı�ͼ�ε���״�ʹ�С��ƽ�ƿ��Բ���ˮƽ�ġ� ƽ�ƻ������ʣ�
����ƽ�ƣ���Ӧ�߶�ƽ�У����ߣ�����ȣ���Ӧ����ȣ���Ӧ�������ӵ��߶�ƽ������ȣ�
ƽ�Ʊ任���ı�ͼ�ε���״����С�ͷ���(ƽ��ǰ�������ͼ����ȫ����)��
��1��ͼ��ƽ��ǰ�����״�ʹ�Сû�б仯��ֻ��λ�÷����仯;
��2��ͼ��ƽ�ƺ�Ӧ�����ɵ��߶�ƽ�У�����ͬһֱ���ϣ������
��3���������ƽ���൱��һ��ƽ�ơ�
��4��ż���ζԳƺ��ͼ�ε���ƽ�ƺ��ͼ�Ρ�
��5��ƽ�����ɷ���;�������ġ�
���ֽ�ͼ���ϵ����е㶼����ij����������ͬ�����λ���ƶ�������ͼ�ε�ƽ���˶������Ϊƽ��
ƽ�Ƶ�������ȷ��һ��ƽ���˶���������ƽ�Ƶķ���;��롣 ƽ�Ƶ�����Ҫ��
1 ԭ����ͼ�ε���״�ʹ�С��ƽ�ƺ��ͼ����ȫ�ȵġ�
2 ƽ�Ƶķ���������������������,��ƫ��n�ȣ���ƫ��n�ȣ���ƫ��n�ȣ���ƫ��n�ȣ�
3 ƽ�Ƶľ��롣�����ȣ���7���ף�8���ȣ� ƽ�����ã�
1.ͨ����ƽ�ƿ��Թ��쾫����ͼ�Ρ�Ҳ���ǻ��ߣ�ͨ������װ�Σ����̾��Ǹ���-ƽ��-ճ����
2.ƽ�Ƴ���ƽ�����й�,ƽ�ƿ��Խ�һ����,һ���߶�,һ��ͼ��ƽ�Ƶ���һ��λ��,�Ƿ�ɢ���������е�һ��ͼ����,ʹ����õ������ ƽ����ͼ�IJ��裺
��1���ҳ��ܱ�ʾͼ�εĹؼ��㣻
��2��ȷ��ƽ�Ƶķ���;��룻
��3����ƽ�Ƶķ���;���ȷ���ؼ���ƽ�ƺ�Ķ�Ӧ�㣻
��4����ԭͼ��˳���������Ӧ�㡣 ��������
- ���ͣ�
- �Ѷȣ�
- ���ˣ�
- �꼶��

 ��У����ϵ�д�
��У����ϵ�д�
 D��
D��
 ��
�� �ĸ��������
�ĸ�������� ��
��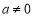 ����ͼ����ͼ��ʾ���Գ���Ϊֱ��
����ͼ����ͼ��ʾ���Գ���Ϊֱ�� �������н��ۣ���
�������н��ۣ��� ��0����
��0����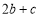 ��0����
��0����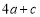 ��
�� ��������ȷ���۵ĸ����ǣ� ��
��������ȷ���۵ĸ����ǣ� ��
 ��k1��0����һ�κ���
��k1��0����һ�κ���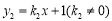 �ཻ��A��B���㣬AC��x���ڵ�C������OAC�����Ϊ1����tan��AOC��2 ��
�ཻ��A��B���㣬AC��x���ڵ�C������OAC�����Ϊ1����tan��AOC��2 ��
 �ķ���
�ķ��� ������˵����ȷ���ǣ� ��.
������˵����ȷ���ǣ� ��.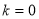 ʱ��������
ʱ��������  ʱ��������������ȵ�ʵ����
ʱ��������������ȵ�ʵ���� ʱ��������һ��ʵ����
ʱ��������һ��ʵ���� 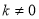 ʱ������������������ȵ�ʵ����
ʱ������������������ȵ�ʵ����