题目内容
 如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是
如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是
- A.S1=S2=S3
- B.S1=S2<S3
- C.S1=S3<S2
- D.S2=S3<S1
A
分析:设直角三角形的三边分别为a、b、c,分别表示出三角形的面积比较即可.
解答: 解:设三角形的三边长分别为a、b、c,
解:设三角形的三边长分别为a、b、c,
∵分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,
∵AE=AB,∠ARE=∠ACB,∠EAR=∠CAB,
∴△AER≌△ACB,
∴ER=BC=a,
FA=b,
∴S1= ab,
ab,
S3= ab,
ab,
同理可得HD=AR=AC,
∴S1=S2=S3=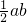 .
.
故选A.
点评:本题考查了解直角三角形及三角形的面积的知识,解题的关键是了解三角形的三边与正方形的边长的关系.
分析:设直角三角形的三边分别为a、b、c,分别表示出三角形的面积比较即可.
解答:
 解:设三角形的三边长分别为a、b、c,
解:设三角形的三边长分别为a、b、c,∵分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,
∵AE=AB,∠ARE=∠ACB,∠EAR=∠CAB,
∴△AER≌△ACB,
∴ER=BC=a,
FA=b,
∴S1=
 ab,
ab,S3=
 ab,
ab,同理可得HD=AR=AC,
∴S1=S2=S3=
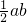 .
.故选A.
点评:本题考查了解直角三角形及三角形的面积的知识,解题的关键是了解三角形的三边与正方形的边长的关系.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB. 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ) 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.