题目内容
5.(1)计算:$\sqrt{0.25}$+$\root{3}{27}$-$\sqrt{\frac{1}{4}+2}$(2)解方程组$\left\{\begin{array}{l}{\frac{1}{3}x+\frac{2}{3}(y-1)=2}\\{2(x-1)=y-1}\end{array}\right.$.
分析 (1)本题涉及二次根式化简、三次根式化简两个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)方程组先化简,再利用加减消元法求出解即可.
解答 解:(1)$\sqrt{0.25}$+$\root{3}{27}$-$\sqrt{\frac{1}{4}+2}$
=0.5+3-$\sqrt{\frac{9}{4}}$
=3.5-1.5
=2;
(2)化简得$\left\{\begin{array}{l}{x+2y=8①}\\{2x-y=1②}\end{array}\right.$,
①+②×2得:5x=10,解得x=2,
把x=2代入①得:y=3,
故原方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$.
点评 本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握二次根式、三次根式等考点的运算.同时考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
13.下列命题中,是真命题的是( )
| A. | 同位角相等 | B. | 有且只有一条直线与已知直线垂直 | ||
| C. | 相等的角是对顶角 | D. | 两条平行线间的距离处处相等 |
20.不等式2x-4<0的解集是( )
| A. | x<2 | B. | x>2 | C. | x≤2 | D. | x≥2 |
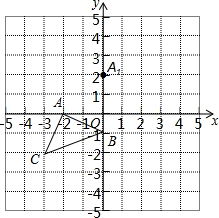 将6×6的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,三角形ABC的顶点和点A,都在格点上.
将6×6的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,三角形ABC的顶点和点A,都在格点上.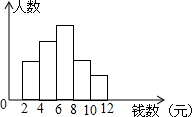 某校七(1)班有48人,对本班学生展开零花钱的消费调查,绘制了如图的频数分布直方图,已知从左到右小长方形高之比为2:3:4:2:1,则零花钱在8元以上的共有12人.
某校七(1)班有48人,对本班学生展开零花钱的消费调查,绘制了如图的频数分布直方图,已知从左到右小长方形高之比为2:3:4:2:1,则零花钱在8元以上的共有12人.