��Ŀ����
����Ŀ����ͼ�٣�ABCD�DZ߳�Ϊ60cm��������ӲֽƬ����ȥ�ĸ�ȫ�ȵĵ���ֱ�������Σ���Ӱ������ʾ��������E��F��AB�ϣ������������𣬵�A��B��C��Dǡ���غ��ڵ�O������ͼ����ʾ�����γ���һ������Ϊ������GHMN�İ�װ�У���AE=x ��cm����
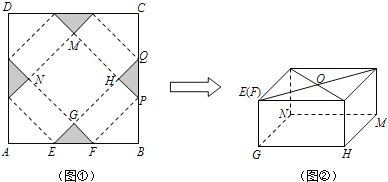
��1�����߶�GF�ij������ú�x�Ĵ���ʽ��ʾ��
��2����xΪ��ֵʱ������GHPF�����S ��cm2�����������Ϊ���٣�
��3�����ʣ����ְ�װ���ܷ����һ������뾶Ϊ15cm����Ϊ10cm��Բ���ι���Ʒ����ʹ��Բ���ι���Ʒ��һ������ǡ������ͼ���е�������GHMN�ڣ����ܣ����������������x��ֵ��Χ�������ܣ���˵�����ɣ�
���𰸡���1��30![]() ��
��![]() x����2����x=15ʱ��S���=450����3��15
x����2����x=15ʱ��S���=450����3��15![]() ��x��30��5
��x��30��5![]() ��
��
��������
�����������1��AE=BF=x���ݴ˼�������x��ʾ������ֱ����EFG��б��EF�ij���Ȼ���������Ǻ������GF�ij���
��2���������þ��ε������ʽ��ʾ�����S��Ȼ�����ö��κ��������ʼ�����⣻
��3����������������θ������е��߶εij��ȣ�Ȼ���жϸ�С�ڻ����10cm�����жϣ�Ȼ�����NG�ij���С��30cm���߲�С��10cm�����в���ʽ���x�ķ�Χ��
�⣺��1����AE=BF=x��
��EF=AB��AE��BF=60��2x��
����Rt��GEF��GF=![]() EF=
EF=![]() ����60��2x��=30
����60��2x��=30![]() ��
��![]() x��
x��
��2����NG=![]() AE=
AE=![]() x����GH=NG=
x����GH=NG=![]() x��
x��
��S=![]() x ��30
x ��30![]() ��
��![]() x��=��2x2+60x
x��=��2x2+60x
=��2��x��15��2+450��
����2��0��
����x=15ʱ��S���=450��
��3���ܷ��£�
�����ǣ���Բ���ι���Ʒ��GHMN����ʱ��x=15![]() ��
��
��ʱ��30![]() ��
��![]() x=30
x=30![]() ��15
��15![]() ��
��![]() =30
=30![]() ��30��10����һ���ܷ��£�
��30��10����һ���ܷ��£�
��������ã�![]()
��ã�15![]() ��x��30��5
��x��30��5![]() ��
��