题目内容
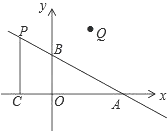
【题目】如图,在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A,B(点A在点B的左侧),与y轴交于点C(0,﹣3).
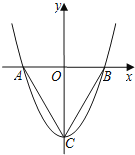
(1)求∠ABC的度数;
(2)若点D是第四象限内抛物线上一点,△ADC的面积为![]() ,求点D的坐标;
,求点D的坐标;
(3)若将△OBC绕平面内某一点顺时针旋转60°得到△O′B′C′,点O′,B′均落在此抛物线上,求此时O′的坐标.
【答案】(1)∠ABC=60°;(2)D (![]() ,
,![]() ).(3)O′(﹣
).(3)O′(﹣![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)通过求函数解析式,求出相应线段的长度,观察AC=2OA,进而求出∠ABC度数;
(2)通过观察三角形ADC面积与三角形AOC面积相等,可以判断直线OD∥AC,求出直线与抛物线交点即为点D;
(3)利用抛物线解析式设出O′,通过旋转60°,求出点B′的坐标,将点B′代入抛物线解析式即可求出.
解:(1)由题意与y轴交于点C(0,﹣3),
∴得解析式为y=x2﹣3,
令y=0,x=±![]() ,
,
∴B(![]() ,0),A(﹣
,0),A(﹣![]() ,0),
,0),
∴OA=![]() ,OC=3,AC=2
,OC=3,AC=2![]() ,
,
∴∠OCA=30°,
∴∠ABC=60°;
(2)由(1)得:OA=![]() ,OC=3,
,OC=3,
∴S△OAC=![]() ×3×
×3×![]() =
=![]() ,
,
过原点与AC平行的直线y=﹣![]() ,
,
直线与抛物线的交点即为点D,
联立:![]() ,
,
解得x1=![]() ,x2=
,x2=![]() (舍去),
(舍去),
∴D (![]() ,
,![]() ).
).
(3)设点O′(m,m2﹣3),
∵顺时针旋转60°,
则点B′(m+![]() ,m2﹣
,m2﹣![]() ),
),
∴(m+![]() )﹣3=m2﹣
)﹣3=m2﹣![]() ,
,
∴m=﹣![]() ,
,
∴O′(﹣![]() ,﹣
,﹣![]() ).
).

练习册系列答案
相关题目