题目内容
在正方形ABCD的边AB、BC、CD、DA上分别任意取点E、F、G、H．这样得到的四边形EFGH中，是正方形的有
- A.1个
- B.2个
- C.4个
- D.无穷多个
D
分析：在正方形四边上任意取点E、F、G、H，若能证明四边形EFGH为正方形，则说明可以得到无穷个正方形．
解答：
解：无穷多个．如图正方形ABCD：
AH=DG=CF=BE，HD=CG=FB=EA，∠A=∠B=∠C=∠D，
有△AEH≌△DHG≌△CGF≌△BFE，
则EH=HG=GF=FE，
另外 很容易得四个角均为90°
则四边形EHGF为正方形．
故选D．
点评：本题考查了正方形的判定与性质，难度适中，利用三角形全等的判定证明EH=HG=GF=FE．
分析：在正方形四边上任意取点E、F、G、H，若能证明四边形EFGH为正方形，则说明可以得到无穷个正方形．
解答：
解：无穷多个．如图正方形ABCD：AH=DG=CF=BE，HD=CG=FB=EA，∠A=∠B=∠C=∠D，
有△AEH≌△DHG≌△CGF≌△BFE，
则EH=HG=GF=FE，
另外 很容易得四个角均为90°
则四边形EHGF为正方形．
故选D．
点评：本题考查了正方形的判定与性质，难度适中，利用三角形全等的判定证明EH=HG=GF=FE．
练习册系列答案
华东师大版一课一练系列答案
相关题目
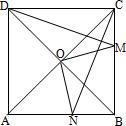42、如图，在正方形ABCD的边BC上任取一点M，过点C作CN⊥DM交AB于N，设正方形对角线交点为O，试确定OM与ON之间的关系，并说明理由．
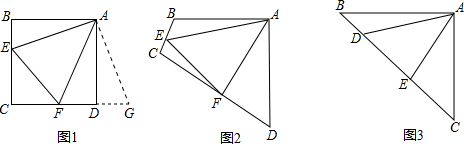
如图，正方形CEFG的对角线CF在正方形ABCD的边BC的延长线上（CE＞BC），点M在CF上，且MF=AB，线段AF与DM交于点N．