题目内容
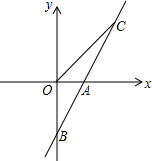 如图,直线AB是一次函数y=kx+b的图象,点A、B的坐标分别为(1,0)、(0,-2)
如图,直线AB是一次函数y=kx+b的图象,点A、B的坐标分别为(1,0)、(0,-2)(1)求直线AB的解析式;
(2)写出不等式kx+b>1的解集;
(3)若直线AB上的点P(m,n)在线段AB上移动,则m,n应如何取值?
(4)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
分析:(1)把点A、B的坐标分别代入一次函数解析式,列出关于系数k、b的方程组,通过解方程组求得它们的值;
(2)通过解不等式2x-2>1即可求得x的取值范围;
(3)根据图象直接回答问题;
(4)设点C的纵坐标为h,S△BOC=S△AOB+S△AOC,所以由三角形的面积公式可以求得h=2.最后把x=2代入直线AB的解析式即可求得点C的纵坐标.
(2)通过解不等式2x-2>1即可求得x的取值范围;
(3)根据图象直接回答问题;
(4)设点C的纵坐标为h,S△BOC=S△AOB+S△AOC,所以由三角形的面积公式可以求得h=2.最后把x=2代入直线AB的解析式即可求得点C的纵坐标.
解答: 解:(1)因为点A、B在函数y=kx+b的图象上,
解:(1)因为点A、B在函数y=kx+b的图象上,
所以
解得
所以直线AB的解析式为y=2x-2;
(2)不等式kx+b>1的解集,即2x-2>1,解得x>
;
(3)0≤m≤1,-2≤n≤0;
(4)设点C的纵坐标为h,S△BOC=S△AOB+S△AOC=
×OA×OB+
×OA×h
=
×1×2+
×1×h=2
所以h=2,
因为点C在直线AB上,所以点C的横坐标为2,
所以点C的坐标为(2,2).
 解:(1)因为点A、B在函数y=kx+b的图象上,
解:(1)因为点A、B在函数y=kx+b的图象上,所以
|
|
所以直线AB的解析式为y=2x-2;
(2)不等式kx+b>1的解集,即2x-2>1,解得x>
| 3 |
| 2 |
(3)0≤m≤1,-2≤n≤0;
(4)设点C的纵坐标为h,S△BOC=S△AOB+S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
所以h=2,
因为点C在直线AB上,所以点C的横坐标为2,
所以点C的坐标为(2,2).
点评:本题考查了待定系数法求一次函数解析式、一次函数图象等.解答(4)题时,采用了“分割法”求三角形的面积.

练习册系列答案
相关题目

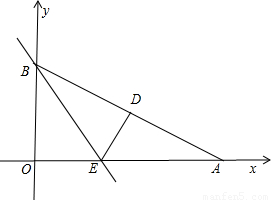
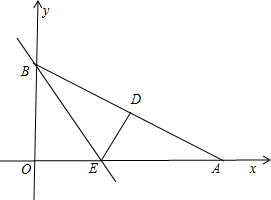 重合,点A在x轴上,点B在y轴上
重合,点A在x轴上,点B在y轴上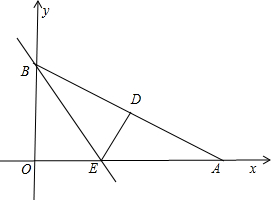 重合,点A在x轴上,点B在y轴上
重合,点A在x轴上,点B在y轴上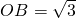 ,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.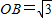 ,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.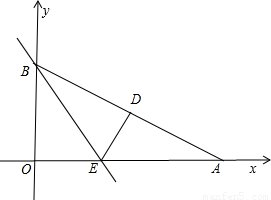
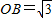 ,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.
,∠BAO=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折痕为BE.