题目内容
已知|a|=2013，|b|=2012；且a+b＜0，求a-b的值．
解：∵|a|=2013，|b|=2012，
∴a=±2013，b=±2012，
∵a+b＜0，
∴a=-2003，b=2012或a=-2013，b=-2012，
∴a-b=-2003-2012=-4025，
或a-b=-2013-（-2012）=-1，
所以a-b的值是-4025或-1．
分析：根据绝对值的性质求出a、b的值，再根据a+b＜0得到a、b的对应值，然后代入求解即可．
点评：本题考查了绝对值的性质，有理数的加法，有理数的减法，是基础题，确定出a、b的对应情况是解题的关键．
∴a=±2013，b=±2012，
∵a+b＜0，
∴a=-2003，b=2012或a=-2013，b=-2012，
∴a-b=-2003-2012=-4025，
或a-b=-2013-（-2012）=-1，
所以a-b的值是-4025或-1．
分析：根据绝对值的性质求出a、b的值，再根据a+b＜0得到a、b的对应值，然后代入求解即可．
点评：本题考查了绝对值的性质，有理数的加法，有理数的减法，是基础题，确定出a、b的对应情况是解题的关键．
练习册系列答案
相关题目
的值。小明觉得直接代入计算太繁了，请你来帮他解决，并写出具体过程。
的值。小明觉得直接代入计算太繁了，请你来帮他解决，并写出具体过程。
÷（1-
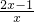）的值．