题目内容
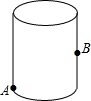 没有上盖的圆柱盒高为10cm,底面周长为32cm,点A距离下底面3cm.一只位于圆柱盒外表面点A处的蚂蚁想爬到盒内表面对侧中点B处.则蚂蚁需要爬行的最短路程的长为
没有上盖的圆柱盒高为10cm,底面周长为32cm,点A距离下底面3cm.一只位于圆柱盒外表面点A处的蚂蚁想爬到盒内表面对侧中点B处.则蚂蚁需要爬行的最短路程的长为考点:平面展开-最短路径问题
专题:
分析:将圆柱侧面展开,得到长方形MNQP,作点B关于PQ的对称点B′,构造直角三角形ACB′,根据勾股定理求出AB′=20cm,即是所求.
解答: 解:如图,点B与点B′关于PQ对称,
解:如图,点B与点B′关于PQ对称,
可得AC=16cm,B′C=12cm,
则最短路程为AB′=
=20cm.
故答案为:20.
 解:如图,点B与点B′关于PQ对称,
解:如图,点B与点B′关于PQ对称,可得AC=16cm,B′C=12cm,
则最短路程为AB′=
| 162+122 |
故答案为:20.
点评:本题考查平面展开最短路径问题,关键知道圆柱展开图是长方形,根据两点之间线段最短可求出解,注意是从圆柱盒外爬到盒内,审准题也是关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
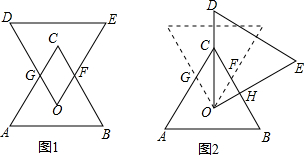 如图(1),有两个全等的正三角形ABC和ODE,点O、C分别为△ABC、△DEO的重心;固定点O,将△ODE顺时针旋转,使得OD经过点C,如图(2),则图(2)中四边形OGCF与△OCH面积的比为
如图(1),有两个全等的正三角形ABC和ODE,点O、C分别为△ABC、△DEO的重心;固定点O,将△ODE顺时针旋转,使得OD经过点C,如图(2),则图(2)中四边形OGCF与△OCH面积的比为如果样本1,2,3,5,x的平均数是3,那么x的值为( )
| A、4 | B、5 | C、3 | D、2 |
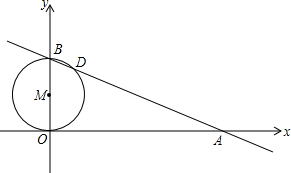 如图,直线
如图,直线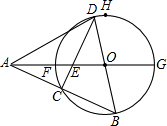 如图,点A在⊙O外,射线AO与⊙O交于F、G两点,点H在⊙O上,FH弧和GH弧为等弧,点D是FH弧上的一个动点(不运动至F),BD是⊙O的直径,连接AB,交⊙O于点C,连接CD,交AO于点E,且OA=
如图,点A在⊙O外,射线AO与⊙O交于F、G两点,点H在⊙O上,FH弧和GH弧为等弧,点D是FH弧上的一个动点(不运动至F),BD是⊙O的直径,连接AB,交⊙O于点C,连接CD,交AO于点E,且OA=