题目内容
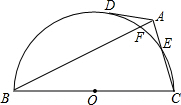 如图,以△ABC的BC边为直径作圆O,分别交AC、AB于E、F两点,过A作圆O的切线,切点为D,并且点E、F为劣弧
如图,以△ABC的BC边为直径作圆O,分别交AC、AB于E、F两点,过A作圆O的切线,切点为D,并且点E、F为劣弧 的三等分点,求∠CAD的大小.
的三等分点,求∠CAD的大小.
 解:连接BE、BD、DF、OD,设圆O半径为r,EC长为l,
解:连接BE、BD、DF、OD,设圆O半径为r,EC长为l,∵E为弧CF的中点,
∴∠ABE=∠CBE,
又∵BE⊥CE,
∴△ABC为等腰三角形,
即AB=BC=2r,AE=EC=l,
∵E,F为弧CD的三等分点,
∴DF=EC=L,
∵AD,AC分别为⊙O的切线和割线,
∴AD2=AE•AC,即AD=
 l,
l,又∵△ADF∽△ABD,
∴
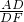 =
= ,
,即BD=
 r,
r,∵BD2=DO2+OB2,
∴∠DBO=45°,
∵∠DBF=∠FBE=∠EBC,
AB=BC,
∴∠ABC=∠DAB=30°,
∠BAC=75°,
∴∠CAD=105°.
分析:根据已知得出△ABC为等腰三角形,进而利用切割线定理求出AD=
 l,从而得出BD=
l,从而得出BD= r,即可得出∠ABC=∠DAB=30°,∠BAC=75°,得出答案.
r,即可得出∠ABC=∠DAB=30°,∠BAC=75°,得出答案.点评:此题主要考查了切线的性质以及全等三角形的性质和圆周角定理,熟练利用切割线定理得出AD=
 l,BD=
l,BD= r是解题关键.
r是解题关键. 
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.
26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.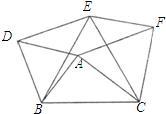 12、如图,以△ABC的三边为边,在BC的同侧作三个等边△ABD、△BEC、△ACF.
12、如图,以△ABC的三边为边,在BC的同侧作三个等边△ABD、△BEC、△ACF.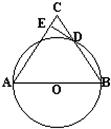 21、如图,以△ABC的边AB为直径作⊙O交BC于D,过D作⊙O的切线交AC于E,要使得DE⊥AC,则△ABC的边必须满足的条件是
21、如图,以△ABC的边AB为直径作⊙O交BC于D,过D作⊙O的切线交AC于E,要使得DE⊥AC,则△ABC的边必须满足的条件是 (2013•玉林)如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
(2013•玉林)如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.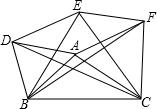 如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF
如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF