题目内容
在矩形ABCD中,点P在AD上,AB=3,AP=1,∠MPN=90°,如图①,当直角边PM经过点B时,另一直角边PN恰好经过点C,将∠MPN从图①的位置开始,绕点P顺时针旋转,PM交射线BA于点E,PN交边BC于点F,当点F与点B重合时停止转动(如图②),在这个过程中,请你观察、探究并解答:

(1)直接写出:线段BC的长度
(2)当点E在线段AB上时.设BE=x,EF2=y,求y关于x的函数关系式,并求当x为何值时,y值最小.最小值为多少?
(3)在整个运动过程中,∠PEF的大小是否发生变化?请说明理由.
(4)直接写出从开始到停止,线段EF的中点经过的路线长.

(1)直接写出:线段BC的长度
10
10
;(2)当点E在线段AB上时.设BE=x,EF2=y,求y关于x的函数关系式,并求当x为何值时,y值最小.最小值为多少?
(3)在整个运动过程中,∠PEF的大小是否发生变化?请说明理由.
(4)直接写出从开始到停止,线段EF的中点经过的路线长.
分析:(1)由在矩形ABCD中,点P在AD上,AB=3,AP=1,∠BPC=90°,易证得△ABP∽△DPC,然后由相似三角形的对应边成比例,即可求得此时PC的长进而求出BC的长;
(2)首先过点F作FG⊥AD于点G.易证得△APE∽△GFP,求出y关于x的函数关系式,再利用配方法求出函数最值即可;
(3)由相似三角形的对应边成比例,易求得tan∠PEF=
=3.即可得∠PEF的大小不发生变化;
(4)如图2,3,画出起始位置和终点位置时,线段EF的中点O1,O2,连接O1O2,线段O1O2即为线段EF的中点经过的路线长,也就是△BPC的中位线.
(2)首先过点F作FG⊥AD于点G.易证得△APE∽△GFP,求出y关于x的函数关系式,再利用配方法求出函数最值即可;
(3)由相似三角形的对应边成比例,易求得tan∠PEF=
| PF |
| PE |
(4)如图2,3,画出起始位置和终点位置时,线段EF的中点O1,O2,连接O1O2,线段O1O2即为线段EF的中点经过的路线长,也就是△BPC的中位线.
解答:解:(1)在矩形ABCD中,∠A=∠D=90°,AP=1,CD=AB=3,
∴PB=
,∠ABP+∠APB=90°.
∵∠BPC=90°,
∴∠APB+∠DPC=90°.
∴∠ABP=∠DPC.
∴△ABP∽△DPC.
∴
=
,
即
=
.
∴PC=3
,
∴线段BC的长度为:BC=
=10;
(2)如图1,过点F作FG⊥AD于点G.
∴四边形ABFG是矩形.
∴∠A=∠AGF=90°.
∴GF=AB=3,∠AEP+∠APE=90°.
∵∠EPF=90°,
∴∠APE+∠GPF=90°.
∴∠AEP=∠GPF.
∴△APE∽△GFP,
∴
=
,
∴
=
,
∴PG=9-3x,
∴AG=BF=10-3x,
∵EF2=BE2+BF2,
∴y=x2+(10-3x)2,
=10x2-60x+100,
=10(x-3) 2+10.
故当x为3时,y值最小,最小值为10.
(3)∠PEF的大小不变.
理由:由(2)得出∵△APE∽△GFP,
∴
=
=
=3.
∴在Rt△EPF中,tan∠PEF=
=3.
即tan∠PEF的值不变.
∴∠PEF的大小不变.
(4)如图2,图3所示:
设线段EF的中点为O,连接OP,OB,
∵在Rt△EPF中,OP=
EF,
在Rt△EBF中,OB=
EF,
∴OP=OB=
EF,
∴O点在线段BP的垂直平分线上,
∴线段EF的中点经过的路线长为O1O2=
PC=
.
故答案为:10.
∴PB=
| 10 |
∵∠BPC=90°,
∴∠APB+∠DPC=90°.
∴∠ABP=∠DPC.
∴△ABP∽△DPC.
∴
| AP |
| CD |
| PB |
| PC |
即
| 1 |
| 3 |
| ||
| PC |
∴PC=3
| 10 |
∴线段BC的长度为:BC=
(
|
(2)如图1,过点F作FG⊥AD于点G.
∴四边形ABFG是矩形.
∴∠A=∠AGF=90°.
∴GF=AB=3,∠AEP+∠APE=90°.
∵∠EPF=90°,
∴∠APE+∠GPF=90°.
∴∠AEP=∠GPF.
∴△APE∽△GFP,
∴
| AE |
| PG |
| AP |
| GF |
∴
| 3-x |
| PG |
| 1 |
| 3 |

∴PG=9-3x,
∴AG=BF=10-3x,
∵EF2=BE2+BF2,
∴y=x2+(10-3x)2,
=10x2-60x+100,
=10(x-3) 2+10.
故当x为3时,y值最小,最小值为10.
(3)∠PEF的大小不变.

理由:由(2)得出∵△APE∽△GFP,
∴
| PF |
| PE |
| GF |
| AP |
| 3 |
| 1 |
∴在Rt△EPF中,tan∠PEF=
| PF |
| PE |
即tan∠PEF的值不变.
∴∠PEF的大小不变.
(4)如图2,图3所示:
设线段EF的中点为O,连接OP,OB,

∵在Rt△EPF中,OP=
| 1 |
| 2 |
在Rt△EBF中,OB=
| 1 |
| 2 |
∴OP=OB=
| 1 |
| 2 |
∴O点在线段BP的垂直平分线上,
∴线段EF的中点经过的路线长为O1O2=
| 1 |
| 2 |
3
| ||
| 2 |
故答案为:10.
点评:此题考查了相似三角形的判定与性质、矩形的性质、勾股定理以及三角函数的性质.此题难度较大,注意掌握数形结合思想的应用.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 1、如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.线段DF与图中的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明.即DF=
1、如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.线段DF与图中的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明.即DF=AB
.(写出一条线段即可) 14、如图所示,在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE于F,若AB=3,BC=5,则四边形DFEC的面积是( )
14、如图所示,在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE于F,若AB=3,BC=5,则四边形DFEC的面积是( )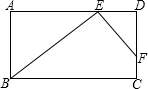
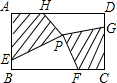 如图,在矩形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,点P在矩形ABCD内,若AB=4,BC=6,AE=CG=3,BF=DH=4,四边形AEPH的面积为5,求四边形PFCG的面积.
如图,在矩形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,点P在矩形ABCD内,若AB=4,BC=6,AE=CG=3,BF=DH=4,四边形AEPH的面积为5,求四边形PFCG的面积. (2013•泰州)如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
(2013•泰州)如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.