题目内容
19．x2+y2+4x-6y+13=0，求$\root{3}{{x}^{3}+{y}^{3}}$的值．分析 利用配方法把已知算式进行变形，根据非负数的性质分别求出x、y的值，代入代数式计算即可．
解答 解：∵x2+y2+4x-6y+13=0，
∴x2+4x+4+y2-6y+9=0，即（x+2）2+（y-3）2=0，
则x+2=0，y-3=0，
解得，x=-2，y=3，
则$\root{3}{{x}^{3}+{y}^{3}}$=$\root{3}{19}$．
点评 本题考查的是配方法的应用，掌握配方法的一般步骤是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
9．已知a+b=4，c-d=-3，则（b-c）-（-d-a）的值为（ ）
| A． | 7 | B． | -7 | C． | 1 | D． | -1 |
10．某校九年级学生从学校去博物馆看展览，学校距离博物馆10千米，一部分同学骑自行车先走，过了20分钟后，其余同学乘汽车出发，结果他们同时到达，已知汽车的速度是骑自行车同学速度的2倍，求骑自行车同学的速度．
（1）设骑车同学的速度为x千米/时，利用速度、时间、路程之间的关系填写下表（要求：填上适当的代数式，完成表格）
（2）列出方程，并求出问题的解．
（1）设骑车同学的速度为x千米/时，利用速度、时间、路程之间的关系填写下表（要求：填上适当的代数式，完成表格）
| 速度（千米/时） | 所用时间（时） | 所走路程（千米） | |
| 骑自行车 | x | $\frac{10}{x}$ | 10 |
| 乘汽车 | 2x | $\frac{10}{2x}$ | 10 |
7．
为增强公民的节约意识，合理利用天然气资源，某市自1月1日起对市区民用管道天然气价格进行调整，实行阶梯式气价，调整后的收费价格如表所示：
（1）若某用户3月份用气量为60m3，交费多少元？
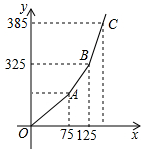
（2）调价后每月支付燃气费用y（单位：元）与每月用气量x（单位：m3）的关系如图所示，求y与x的解析式及a的值．
为增强公民的节约意识，合理利用天然气资源，某市自1月1日起对市区民用管道天然气价格进行调整，实行阶梯式气价，调整后的收费价格如表所示：| 每月用气量 | 单价（元/m3） |
| 不超出75m3的部分 | 2.5 |
| 超出75m3不超过125m3的部分 | a |
| 超出125m3的部分 | a+0.25 |
（2）调价后每月支付燃气费用y（单位：元）与每月用气量x（单位：m3）的关系如图所示，求y与x的解析式及a的值．
14．下列计算正确的是（ ）
| A． | $\sqrt{（-2）^{2}}$=-2 | B． | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | C． | 2÷$\sqrt{2}$=$\sqrt{2}$ | D． | 2$\sqrt{2}$-$\sqrt{2}$=2 |
4．期中考试后，两位同学讨论他们所在小组的数学成绩，小明说：“我们组7位同学中，有4人的成绩是86分”，小亮说：“我们组7位同学中，第4名的成绩是86分”，上面两位同学所说的“86分”反映的统计量分别是（ ）
| A． | 众数和中位数 | B． | 众数与平均数 | C． | 众数和方差 | D． | 平均数与中位数 |
11．下列说法中，正确的是（ ）
| A． | 两条对角线相等的四边形是平行四边形 | |
| B． | 两条对角线相等且互相垂直的四边形是矩形 | |
| C． | 两条对角线互相垂直平分的四边形是菱形 | |
| D． | 两条对角线互相垂直平分且相等的四边形是菱形 |