题目内容
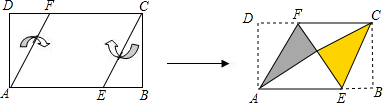
将矩形纸片ABCD按如图方式折叠,DE、CF为折痕,折叠后点A和点B都落在点O处.若△EOF是等边三角形,则 的值为 .
的值为 .
【答案】分析:由△EOF是等边三角形,可得EF=OE=OF,∠OEF=60°,又由由折叠的性质可得:OE=AE,OF=BF,∠AED=∠OED,则可得AB=3AE,∠AED=60°,则可证得AD= AE,继而求得答案.
AE,继而求得答案.
解答:解:∵△EOF是等边三角形,
∴EF=OE=OF,∠OEF=60°,
由折叠的性质可得:OE=AE,OF=BF,∠AED=∠OED,
∴AB=3AE,∠AED= =60°,
=60°,
∵四边形ABCD是矩形,
∴∠A=90°,
∴tan∠AED= =
= ,
,
∴AD= AE,
AE,
∴ =
= =
= .
.
故答案为: .
.
点评:此题考查了折叠的性质、等边三角形的性质、矩形的性质以及三角函数等知识.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.
 AE,继而求得答案.
AE,继而求得答案.解答:解:∵△EOF是等边三角形,
∴EF=OE=OF,∠OEF=60°,
由折叠的性质可得:OE=AE,OF=BF,∠AED=∠OED,
∴AB=3AE,∠AED=
 =60°,
=60°,∵四边形ABCD是矩形,
∴∠A=90°,
∴tan∠AED=
 =
= ,
,∴AD=
 AE,
AE,∴
 =
= =
= .
.故答案为:
 .
.点评:此题考查了折叠的性质、等边三角形的性质、矩形的性质以及三角函数等知识.此题难度适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
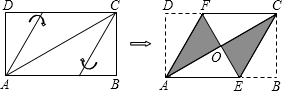
将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为( )

| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
 C的长为
C的长为

