题目内容
在口袋中装有23个号码球,分别标有1~23共23个数字,各小球除了号码不同外完全相同,现在从中随意取出两个小球,求:
(1)第一次取出的小球号码大于9的概率;
(2)第一次取出的小球号码小于30的概率;
(3)如果第一次取出的小球是3,不放回,求第二次取出的小球号码大于9的概率;
(4)如果第一次取出的小球是6,也不放回,再求第二次取出的小球号码是偶数的概率.
解:(1)由题意知:在1~23中,大于9的有10~23共14个数字.
则第一次取出的小球号码大于9的概率为 ;
;
(2)号码全部小于30
故第一次取出的小球号码小于30的概率为1;
(3)取出一个小球3后,大于9的仍有10~23共14个数字
则第二次取出的小球号码大于9的概率为 =
= ;
;
(4)取出一个小球6后,偶数为10个
则第二次取出的小球号码是偶数的概率为 =
=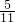 .
.
分析:可以采用列举法.在1~23中,大于9的有10~23共14个数字,全部小于30;取出一个小球3后,大于9的仍有10~23共14个数字,只是总量变成了22,利用概率公式进行计算;取出一个小球6后,总量为22,偶数为10个,也利用概率的公式进行计算即可.
点评:根据随机事件概率大小的求法,找准两点:
①符合条件的情况数目;
②全部情况的总数.
二者的比值就是其发生的概率的大小.
则第一次取出的小球号码大于9的概率为
 ;
;(2)号码全部小于30
故第一次取出的小球号码小于30的概率为1;
(3)取出一个小球3后,大于9的仍有10~23共14个数字
则第二次取出的小球号码大于9的概率为
 =
= ;
;(4)取出一个小球6后,偶数为10个
则第二次取出的小球号码是偶数的概率为
 =
=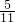 .
.分析:可以采用列举法.在1~23中,大于9的有10~23共14个数字,全部小于30;取出一个小球3后,大于9的仍有10~23共14个数字,只是总量变成了22,利用概率公式进行计算;取出一个小球6后,总量为22,偶数为10个,也利用概率的公式进行计算即可.
点评:根据随机事件概率大小的求法,找准两点:
①符合条件的情况数目;
②全部情况的总数.
二者的比值就是其发生的概率的大小.

练习册系列答案
相关题目
 下列说法中,你认为正确的是( )
下列说法中,你认为正确的是( )A、一口袋中装有99个红球,1个黑球,则摸一次摸到黑球的概率为
| ||
| B、如图所示是可以自由转动的转盘,它平均每转6次,指针可能有5次落在黑色区域 | ||
| C、小明前五次掷硬币都是正面朝上,则他肯定地说第六次掷还是正面朝上 | ||
| D、某次摸奖的中奖率是1%,则只要摸奖100张,一定有一张中奖 |
在一个不透明的口袋中,装有若干个除颜色外其余都相同的球,如果口袋中装有4个红球且摸到红球的概率为
,那么口袋中球的总数为( )
| 1 |
| 2 |
| A、8个 | B、6个 | C、4个 | D、2个 |