题目内容
 如图,已知在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
如图,已知在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)说明△ADC≌△CEB;
(2)说明AD+BE=DE.
考点:全等三角形的判定与性质,等腰直角三角形
专题:几何图形问题,证明题
分析:(1)根据垂直的性质就可以得出∠ADC=∠CEB=90°,由直角三角形的性质就可以得出∠DAC=∠ECB,就可以得出△ADC≌△CEB;
(2)根据△ADC≌△CEB就可以得出AD=CE,CD=BE.就可以得出结论.
(2)根据△ADC≌△CEB就可以得出AD=CE,CD=BE.就可以得出结论.
解答:解:(1)∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°.
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∴∠DAC=∠ECB.
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS)
(2)∵△ADC≌△CEB,
∴AD=CE,CD=BE.
∵DE=CD+CE,
∴DE=AD+BE.
∴∠ADC=∠CEB=90°,

∴∠DAC+∠ACD=90°.
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∴∠DAC=∠ECB.
在△ADC和△CEB中,
|
∴△ADC≌△CEB(AAS)
(2)∵△ADC≌△CEB,
∴AD=CE,CD=BE.
∵DE=CD+CE,
∴DE=AD+BE.
点评:本题考查了垂直的性质的运用,直角三角形的性质的运用,直角三角形的性质的运用,全等三角形的判定及性质的运用.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目

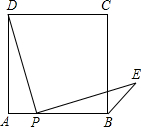 点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得到线段PE,连接BE,则∠CBE等于
点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得到线段PE,连接BE,则∠CBE等于