题目内容
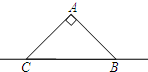
 如图,在△ACB=∠90°,AB的垂直平分线DE交AB于E,交AC于D,∠DBC=30°,BD=4.8cm,则D到AB的距离为
如图,在△ACB=∠90°,AB的垂直平分线DE交AB于E,交AC于D,∠DBC=30°,BD=4.8cm,则D到AB的距离为分析:先根据线段的垂直平分线的性质得到DB=DA,则有∠A=∠ABD,而∠C=90°,∠DBC=30°,利用三角形的内角和可得∠A+∠ABD=90°-30°=60°,得到∠ABD=30°,在Rt△BED中根据含30°的直角三角形三边的关系即可得到DE=
BD=2.4cm.
| 1 |
| 2 |
解答:解:∵DE垂直平分AB,
∴DB=DA,
∴∠A=∠ABD,
而∠C=90°,∠DBC=30°,
∴∠A+∠ABD=90°-30°=60°,
∴∠ABD=30°,
在Rt△BED中,∠EBD=30°,BD=4.8cm,
∴DE=
BD=2.4cm,
即D到AB的距离为2.4cm.
故答案为2.4.
∴DB=DA,
∴∠A=∠ABD,
而∠C=90°,∠DBC=30°,
∴∠A+∠ABD=90°-30°=60°,
∴∠ABD=30°,
在Rt△BED中,∠EBD=30°,BD=4.8cm,
∴DE=
| 1 |
| 2 |
即D到AB的距离为2.4cm.
故答案为2.4.
点评:本题考查了线段的垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等.也考查了含30°的直角三角形三边的关系.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 (2012•虹口区二模)如图,在△ACB中,∠CAB=90°,AC=AB=3,将△ABC沿直线BC平移,顶点A、C、B平移后分别记为A1、C1、B1,若△ACB与△A1C1B1重合部分的面积2,则CB1=
(2012•虹口区二模)如图,在△ACB中,∠CAB=90°,AC=AB=3,将△ABC沿直线BC平移,顶点A、C、B平移后分别记为A1、C1、B1,若△ACB与△A1C1B1重合部分的面积2,则CB1= 如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-6,3),则B点的坐标是
如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-6,3),则B点的坐标是 如图:在△ACB中,点D是AB边上一点,且∠ACB=∠CDA,∠CAB的平分线分别交CD、BC于点E、F.
如图:在△ACB中,点D是AB边上一点,且∠ACB=∠CDA,∠CAB的平分线分别交CD、BC于点E、F. 如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.
如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.