题目内容
12.已知一次函数的图象经过点A(1,1)和点B(2,-1),求这个一次函数的解析式.分析 利用待定系数法把A(1,1)和点B(2,-1),代入一次函数y=kx+b,可得到一个关于k、b的方程组,再解方程组即可得到k、b的值,然后即可得到一次函数的解析式.
解答 解:设一次函数y=kx+b的图象经过两点A(1,1),B(2,-1),
∵A(1,1)和点B(2,-1),
∴$\left\{\begin{array}{l}{1=k+b}\\{-1=2k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=3}\end{array}\right.$,
∴一次函数解析式为:y=-2x+3.
点评 此题主要考查了待定系数法求一次函数解析式,关键是掌握待定系数法求一次函数解析式一般步骤是:(1)先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;(2)将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;(3)解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
相关题目
20.正比例函数y=-2x的图象经过的点是( )
| A. | (1,2) | B. | (1,-2) | C. | (-2,1) | D. | (-2,-1) |
17.若(x-1)2-9=0,则x=( )
| A. | ±9 | B. | ±3 | C. | 4或-2 | D. | -4或2 |
1.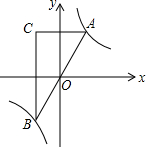 如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )
如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )
 如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )
如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )| A. | n=-2m | B. | n=-$\frac{2}{m}$ | C. | n=-4m | D. | n=-$\frac{4}{m}$ |
2.学校举办的环保知识竞赛,规定每班5位同学参加.初二(1)班选派A,B,C,D,E五位同学参加学校举办的环保知识竞赛,竞赛试卷中共有20道题,规定:答对1题得5分,答错1题倒扣2分,未答题得0分.赛后A,B,C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有4道题未答),具体如表:
(1)根据以上信息,求A,B,C,D四位同学竞赛预计成绩的平均分;
(2)最后公布初二(1)班A,B,C,D,E五位同学以总成绩403分获得团体冠军,E同学的成绩是73分获得个人三等奖.
①求E同学的答对题数和答错题数;
②经核对A,B,C,D四位同学实际成绩与(1)中以及成绩对照,发现只有一位同学记错了自己的答题情况,而且还未获得个人奖项,请指出是哪位同学记错了,并写出他的实际答题情况(直接写出答案即可).
| 参赛同学 | A | B | C | D | E |
| 答对题数 | 19 | 17 | 16 | 17 | / |
| 答错题数 | 0 | 2 | 1 | 1 | / |
| 未答题数 | 1 | 1 | 3 | 2 | 4 |
(2)最后公布初二(1)班A,B,C,D,E五位同学以总成绩403分获得团体冠军,E同学的成绩是73分获得个人三等奖.
①求E同学的答对题数和答错题数;
②经核对A,B,C,D四位同学实际成绩与(1)中以及成绩对照,发现只有一位同学记错了自己的答题情况,而且还未获得个人奖项,请指出是哪位同学记错了,并写出他的实际答题情况(直接写出答案即可).
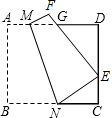 如图,将边长为8的正方形纸片ABCD折叠,使点B落在CD边的中点E上,压平后得到折痕MN,EF与AD边交于点G.
如图,将边长为8的正方形纸片ABCD折叠,使点B落在CD边的中点E上,压平后得到折痕MN,EF与AD边交于点G.