题目内容
 为了利用开发海洋资源,某勘测飞机欲测量一岛屿的两端A、B的距离,飞机在距海平面垂直高度300米的C处测得端点A的俯角为60°,然后飞机沿着俯角30°的方向俯冲到D点,发现端点B的俯角为45°,而此时飞机距离海平面的垂直高度为100米,求岛屿两端A、B的距离.(结果精确到0.1米,
为了利用开发海洋资源,某勘测飞机欲测量一岛屿的两端A、B的距离,飞机在距海平面垂直高度300米的C处测得端点A的俯角为60°,然后飞机沿着俯角30°的方向俯冲到D点,发现端点B的俯角为45°,而此时飞机距离海平面的垂直高度为100米,求岛屿两端A、B的距离.(结果精确到0.1米, ≈1.73,
≈1.73, ≈1.41)
≈1.41)
解:如图,设CG⊥AB于G,过点D作DM⊥AB于M,DN⊥CG于N,

由题意得:CG=300米,DM=100米,∠ACP=60°,∠DCP=30°,∠BDQ=45°,
故可得∠NCD=60°,∠ACG=30°,∠BDM=45°,CN=300-100=200米,
在Rt△DCN中,tan∠CDN= ,则DN=CNtan∠CDN=200
,则DN=CNtan∠CDN=200 米,
米,
在Rt△ACG中,tan∠ACG=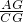 ,则AG=CGtan∠ACG=300×
,则AG=CGtan∠ACG=300× =100
=100 米,
米,
在Rt△BDM中,tan∠BDM=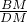 ,则BM=DMtan∠BDM=100米,
,则BM=DMtan∠BDM=100米,
又∵GM=DN,
∴AB=DN+BM-AG=200 +100-100
+100-100 =100
=100 +100≈273米.
+100≈273米.
答:岛屿两端A、B的距离约273米.
分析:设CG⊥AB于G,过点D作DM⊥AB于M,DN⊥CG于N,在Rt△DCN中求出ND,在Rt△ACG中求出AG,在Rt△BDM中求出MB,继而可得出AB的长度.
点评:本题考查了解直角三角形的应用,仰角俯角的知识,解答本题的关键是构造直角三角形,利用解直角三角形的知识求出相关线段的长度.

由题意得:CG=300米,DM=100米,∠ACP=60°,∠DCP=30°,∠BDQ=45°,
故可得∠NCD=60°,∠ACG=30°,∠BDM=45°,CN=300-100=200米,
在Rt△DCN中,tan∠CDN=
 ,则DN=CNtan∠CDN=200
,则DN=CNtan∠CDN=200 米,
米,在Rt△ACG中,tan∠ACG=
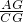 ,则AG=CGtan∠ACG=300×
,则AG=CGtan∠ACG=300× =100
=100 米,
米,在Rt△BDM中,tan∠BDM=
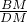 ,则BM=DMtan∠BDM=100米,
,则BM=DMtan∠BDM=100米,又∵GM=DN,
∴AB=DN+BM-AG=200
 +100-100
+100-100 =100
=100 +100≈273米.
+100≈273米.答:岛屿两端A、B的距离约273米.
分析:设CG⊥AB于G,过点D作DM⊥AB于M,DN⊥CG于N,在Rt△DCN中求出ND,在Rt△ACG中求出AG,在Rt△BDM中求出MB,继而可得出AB的长度.
点评:本题考查了解直角三角形的应用,仰角俯角的知识,解答本题的关键是构造直角三角形,利用解直角三角形的知识求出相关线段的长度.

练习册系列答案
相关题目
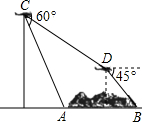 (2013•黄冈模拟)为了利用开发海洋资源,某勘测飞机欲测量一岛屿的两端A、B的距离,飞机在距海平面垂直高度300米的C处测得端点A的俯角为60°,然后飞机沿着俯角30°的方向俯冲到D点,发现端点B的俯角为45°,而此时飞机距离海平面的垂直高度为100米,求岛屿两端A、B的距离.(结果精确到0.1米,
(2013•黄冈模拟)为了利用开发海洋资源,某勘测飞机欲测量一岛屿的两端A、B的距离,飞机在距海平面垂直高度300米的C处测得端点A的俯角为60°,然后飞机沿着俯角30°的方向俯冲到D点,发现端点B的俯角为45°,而此时飞机距离海平面的垂直高度为100米,求岛屿两端A、B的距离.(结果精确到0.1米, (2013•崇左)自古以来,钓鱼岛及其附属岛屿都是我国固有领土.如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A、B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了800米,在点D测得端点B的俯角为45°,求北小岛两侧端点A、B的距离.
(2013•崇左)自古以来,钓鱼岛及其附属岛屿都是我国固有领土.如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A、B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了800米,在点D测得端点B的俯角为45°,求北小岛两侧端点A、B的距离. (2012•山西)如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A、B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,求岛屿两端A、B的距离(结果精确到0.1米,参考数据:
(2012•山西)如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A、B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,求岛屿两端A、B的距离(结果精确到0.1米,参考数据: