题目内容
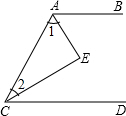 如图:AE平分∠BAC,CE平分∠ACD,且AB∥CD.求证:∠1+∠2=90°.
如图:AE平分∠BAC,CE平分∠ACD,且AB∥CD.求证:∠1+∠2=90°.请完成下面的填空:
证明:∵AB∥CD,(已知)
∴∠BAC+∠ACD=180°.(
又AE平分∠BAC,CE平分∠ACD,(
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1+∠2=
| 1 |
| 2 |
=
| 1 |
| 2 |
=90°
即∠1+∠2=90°.
考点:平行线的性质
专题:推理填空题
分析:由平行的性质可得∠BAC+∠ACD=180°,结合角平分线的定义可得∠1+∠2=90°,依次填空即可.
解答:证明:∵AB∥CD,(已知),
∴∠BAC+∠ACD=180°.( 两直线平行,同旁内角互补).
又AE平分∠BAC,CE平分∠ACD,( 已知).
∴∠1=
∠BAC,∠2=
∠ACD.( 角平分线的定义).
∴∠1+∠2=
∠BAC+∠ACD
=
×180°
=90°
即∠1+∠2=90°.
故答案为:两直线平行,同旁内角互补;已知;角平分线的定义.
∴∠BAC+∠ACD=180°.( 两直线平行,同旁内角互补).
又AE平分∠BAC,CE平分∠ACD,( 已知).
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1+∠2=
| 1 |
| 2 |
=
| 1 |
| 2 |
=90°
即∠1+∠2=90°.
故答案为:两直线平行,同旁内角互补;已知;角平分线的定义.
点评:本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
相关题目
 如图,a∥b,∠A的度数是多少?
如图,a∥b,∠A的度数是多少?