Question

【题目】在平面直角坐标系中，点的坐标为，点在第一象限且点的纵坐标为．当是腰长为的等腰三角形时，则点的坐标为_____．

Answer 1

【答案】或或．

【解析】

分三种情况(1)PD=OD=5，点P在点D左侧；(2)OP=OD=5；(3)PD=OD=5，点P在点D的右侧；分别进行讨论求出点P坐标.

(1)

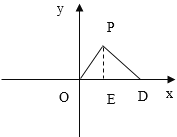
如图所示PD=OD=5，点P在点D左侧，过点P作PE⊥x轴与点E，则PE=4，

在RT△PDE中，由勾股定理得，DE=，

∴OE=OD-DE=5-3=2，

∴此时点P坐标为；

(2)

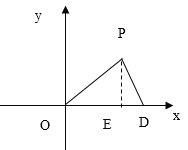
如图所示，OP=OD=5，过点P作PE⊥x轴与点E，则PE=4，

在RT△POE中，由勾股定理得，OE=，

∴此时点P的坐标为；

(3)

如图所示，PD=OD=5，点P在点D的右侧，过点P作PE⊥x轴与点E，则PE=4，

在RT△PDE中，由勾股定理得，DE=，

∴OE=OD+DE=5+3=8，

∴此时点P的坐标为.