题目内容
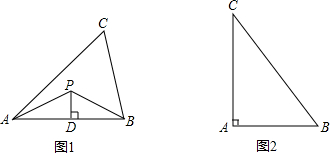
22、(1)如图1,PA,PB分别与圆O相切于点A,B.求证:PA=PB;
(2)如图2,过圆O外一点P的两条直线分别与圆O相交于点A、B和C、D.则当

(2)如图2,过圆O外一点P的两条直线分别与圆O相交于点A、B和C、D.则当
∠BPO=∠DPO
时,PB=PD.(不添加字母符号和辅助线,不需证明,只需填上符合题意的一个条件)
分析:(1)连接OA、OB.则OA⊥PA,OB⊥PB.根据HL证明△POA≌△POB,得证;
(2)若PB=PD,则易证△POB≌△POD,有∠BPO=∠DPO.所以可填∠BPO=∠DPO.
(2)若PB=PD,则易证△POB≌△POD,有∠BPO=∠DPO.所以可填∠BPO=∠DPO.
解答: (1)证明:连接OA、OB.
(1)证明:连接OA、OB.
∵PA、PB是切线,
∴OA⊥PA,OB⊥PB.
∵OA=OB,OP公共,
∴△POA≌△POB,
∴PA=PB.
(2)当∠BPO=∠DPO时,PB=PD.
证明:作OM⊥AB于M,ON⊥CD于N.
∵∠BPO=∠DPO,
∴OM=ON.
∴AB=CD.则BM=DN.
∵OM=ON,OP公共,
∴△POM≌△PON,
∴PM=PN.
∴PB=PD.
 (1)证明:连接OA、OB.
(1)证明:连接OA、OB.∵PA、PB是切线,
∴OA⊥PA,OB⊥PB.
∵OA=OB,OP公共,
∴△POA≌△POB,
∴PA=PB.
(2)当∠BPO=∠DPO时,PB=PD.
证明:作OM⊥AB于M,ON⊥CD于N.
∵∠BPO=∠DPO,
∴OM=ON.
∴AB=CD.则BM=DN.
∵OM=ON,OP公共,
∴△POM≌△PON,
∴PM=PN.
∴PB=PD.
点评:此题考查了切线的性质,拓展题难度也不大.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
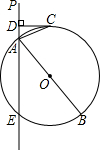 已知:如图,直线PA交⊙O于A、E两点,PA的垂线DC切⊙O于点C,过A点作⊙O的直径AB.
已知:如图,直线PA交⊙O于A、E两点,PA的垂线DC切⊙O于点C,过A点作⊙O的直径AB. 如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB=
如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象.若PA与y轴交于点Q,且S四边形PQOB=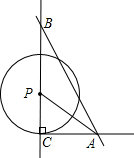 (2012•开平区一模)在Rt△ABC中,∠ACB=90°,AC=4cm,BC=8cm,以点P为圆心,以3cm长为半径的圆在直线BC上滑动.
(2012•开平区一模)在Rt△ABC中,∠ACB=90°,AC=4cm,BC=8cm,以点P为圆心,以3cm长为半径的圆在直线BC上滑动.