Question

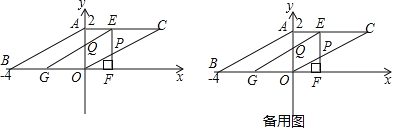
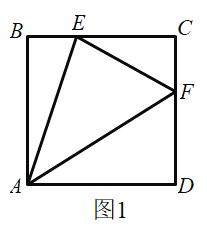
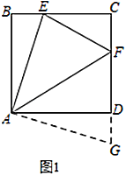
【题目】（1）如图1，在正方形中，点、分别是、边上的动点，且，求证：．

　　　

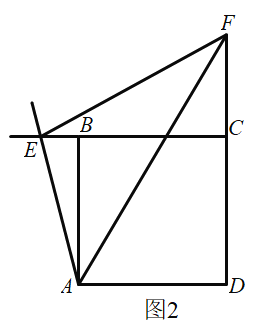
（2）如图2，在正方形中，如果点、分别是、延长线上的动点，且，则、、之间数量关系是什么？请写出证明过程．

（3）如图1，若正方形的边长为6，，求的长．

Answer 1

【答案】（1）见解析；（2）；证明见解析；（3）．

【解析】

（1）把ABE绕点A顺时针旋转90°至ADG，由“SAS”可证EAF≌GAF，可得出EF＝FG，则结论得证；

（2）将ABE绕点A顺时针旋转90°至△ADM，根据SAS可证明EAF≌MAF，可得EF＝FM，则结论得证；

（3）由全等三角形的性质可得AE＝AG＝3，EF＝FG，BE＝DG，由勾股定理可求DG的长，FD的长，AF的长．

（1）证明：把绕点顺时针旋转90°至，

如图1，∴，，

∵，

∴，

∴，

∴，

∵，

∴，

∴，

∴；

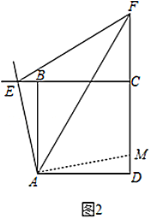
（2）结论：；

证明：如图2，将绕点顺时针旋转90°至，

∴，，，，

∴，

∵，

∴，

∴；

（3）解：由（1）可知，

∵正方形的边长为6，

∴，

∴．

∴，

∴，

设，则，，

在中，∵，

∴，

解得：．

∴，

∴．