��Ŀ����
����Ŀ��С������ѧϰ�����ľ��飬�Ժ���y��x+![]() ��ͼ�������ʽ�����̽����
��ͼ�������ʽ�����̽����
������С����̽�����̣��벹��������
��1������y��x+![]() ���Ա���x��ȡֵ��Χ���� ����
���Ա���x��ȡֵ��Χ���� ����
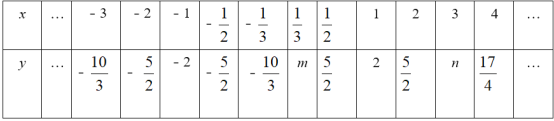
��2���±��г���y��x�ļ����Ӧֵ����д��m��n��ֵ��m���� ����n���� ����
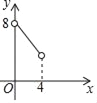
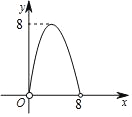
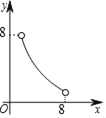
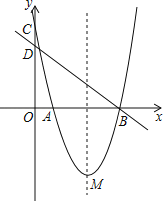
��3����ͼ����ƽ��ֱ������ϵxOy�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣬��������ĵ㣬�����ú�����ͼ��
��4����Ϻ�����ͼ������ɣ�
�ٵ�y����![]() ʱ��x���� ����
ʱ��x���� ����
��д���ú�����һ�������� ����
��������x+![]() ��t����������ȵ�ʵ��������t��ȡֵ��Χ���� ����
��t����������ȵ�ʵ��������t��ȡֵ��Χ���� ����
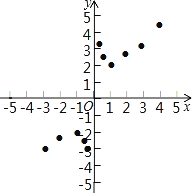
���𰸡���1��![]() ����2��
����2��![]() ����3������������4���٩�4��
����3������������4���٩�4��![]() ����ͼ����һ�������ޣ��ҹ���ԭ��Գƣ���
����ͼ����һ�������ޣ��ҹ���ԭ��Գƣ���![]() ��
��![]()
��������
��1����x�ڷ�ĸ�ϣ��ɵó�x��0��
��2����x��![]() ��3�ֱ����y��x+
��3�ֱ����y��x+![]() �������m��n��ֵ��
�������m��n��ֵ��
��3����������ɻ�������ͼ��
��4���ٰ�y����![]() ���뺯����ϵʽ���ⷽ�̼������xֵ��
���뺯����ϵʽ���ⷽ�̼������xֵ��
�ڿɴӺ���ͼ���λ�úͶԳ��ԵĽǶȽ��
�ۿ������ú���ͼ���ҳ�����y��x+![]() ��y��t����������ʱt��ȡֵ��Χ���ɣ�
��y��t����������ʱt��ȡֵ��Χ���ɣ�
�⣺��1����x�ڷ�ĸ�ϣ���x��0��
�ʴ�Ϊ��x��0��
��2����x��![]() ʱ��y��x+
ʱ��y��x+![]() ��
��![]() ��
��
��x��3ʱ��y��x+![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
��3������ͼ����ͼ��ʾ��
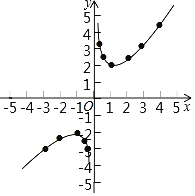
��4���ٵ�y����![]() ʱ����x+
ʱ����x+![]() ����
����![]() ��
��
��ã�x1����4��x2����![]() ��
��
�ʴ�Ϊ����4��![]() ��
��
�ڹ۲캯��ͼ���֪������ͼ���ڵ�һ���������ҹ���ԭ��Գƣ�
�ʴ�Ϊ������ͼ���ڵ�һ���������ҹ���ԭ��Գƣ�
�ۡ�x+![]() ��t����������ȵ�ʵ������������y��x+
��t����������ȵ�ʵ������������y��x+![]() ��y��t���������㣬
��y��t���������㣬
����ͼ��ɵã�t����2��t��2��
�ʴ�Ϊ��t����2��t��2��

 ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д� ����5��2���ϵ�д�
����5��2���ϵ�д�