题目内容
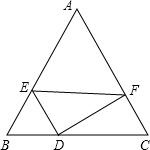如图，D是等边△ABC的边BC上一动点，ED∥AC交AB于点E．DF⊥AC交AC于点F，DF=| 3 |
1或3
1或3
．分析：根据△DCF与E、F、D三点组成的三角形相似，分△DCF∽△EFD和△DCF∽△FED两种情况分类讨论即可得到两个不同的答案．
解答：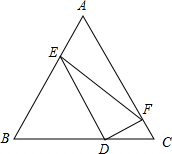
解：∵ED∥AC交AB于点E，△ABC是等边三角形，
∴△BDE是等边三角形，∠FDC=30°，
当△DCF∽△EFD，
∴∠FED=∠FDC=30°
∴DE=
=
=3，
∴BD=DE=3；
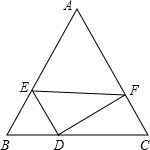当△DCF∽△FED，
∴∠EFD=∠FDC=30°，
∴BD=DE=DF•tan∠A=
×
=1．
故答案为：1或3．
解：∵ED∥AC交AB于点E，△ABC是等边三角形，∴△BDE是等边三角形，∠FDC=30°，
当△DCF∽△EFD，
∴∠FED=∠FDC=30°
∴DE=
| DF |
| tan∠FED |
| ||||
|
∴BD=DE=3；
当△DCF∽△FED，∴∠EFD=∠FDC=30°，
∴BD=DE=DF•tan∠A=
| 3 |
| ||
| 3 |
故答案为：1或3．
点评：本题考查了相似三角形的性质及等边三角形的性质，解题的关键是分两种情况讨论．
练习册系列答案
相关题目
如图，△ABC是等边三角形，AB=4cm，则BC边上的高AD等于
如图，△ABC是等边三角形，点D是线段BC上的一个动点（点D不与点B、C重合），△ADE是以AD为边的等边三角形，过点E作BC的平行线，分别交AB、AC于点F、G，连接BE．
如图，△ABC是等边三角形，CE是外角平分线，点D在AC上，连结BD并延长与CE交于点E．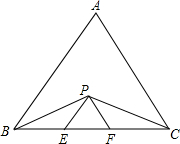
如图，△ABC是等边三角形，P为△ABC内任意一点，PE∥AB，PF∥AC．那么，△PEF是什么三角形？说明理由．