题目内容
 如图,一个含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到△A′B′C的位置,若BC的长为15cm,那么AA’的长为
如图,一个含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到△A′B′C的位置,若BC的长为15cm,那么AA’的长为
- A.10
 cm
cm - B.15
 cm
cm - C.30
 cm
cm - D.30cm
C
分析:连接AA′.构建Rt△ABA′;由旋转的性质可以推知BC=B′C,AC=A′C;根据图示知Rt△ABC中的∠A=30°,由30°所对的直角边是斜边的一半可以求得AC=30cm,由勾股定理可以求得
AB=15 cm;最后在根据线段间的和差关系求得A′B=BC+CA′=BC+AC=45cm,根据勾股定理在Rt△ABA′中求得AA′的值即可.
cm;最后在根据线段间的和差关系求得A′B=BC+CA′=BC+AC=45cm,根据勾股定理在Rt△ABA′中求得AA′的值即可.
解答: 解:连接AA′.
解:连接AA′.
∵△A′B′C是由△ABC按顺时针方向旋转得到的,
∴BC=B′C,AC=A′C;
又∵△ABC是含有一个30°角的直角三角形,
∴从图中知,∠BAC=30°,
∴AC=2BC,AB= BC;
BC;
而BC=15cm;
∴在Rt△ABA′中,
AB=15 cm,A′B=BC+CA′=BC+AC=45cm,
cm,A′B=BC+CA′=BC+AC=45cm,
∴AA′= =30
=30 cm.
cm.
故选C.
点评:本题综合考查了勾股定理、含30°角的直角三角形以及旋转的性质.在直角三角形中,30度角所对的直角边等于斜边的一半,也是解决问题的关键.
分析:连接AA′.构建Rt△ABA′;由旋转的性质可以推知BC=B′C,AC=A′C;根据图示知Rt△ABC中的∠A=30°,由30°所对的直角边是斜边的一半可以求得AC=30cm,由勾股定理可以求得
AB=15
 cm;最后在根据线段间的和差关系求得A′B=BC+CA′=BC+AC=45cm,根据勾股定理在Rt△ABA′中求得AA′的值即可.
cm;最后在根据线段间的和差关系求得A′B=BC+CA′=BC+AC=45cm,根据勾股定理在Rt△ABA′中求得AA′的值即可.解答:
 解:连接AA′.
解:连接AA′.∵△A′B′C是由△ABC按顺时针方向旋转得到的,
∴BC=B′C,AC=A′C;
又∵△ABC是含有一个30°角的直角三角形,
∴从图中知,∠BAC=30°,
∴AC=2BC,AB=
 BC;
BC;而BC=15cm;
∴在Rt△ABA′中,
AB=15
 cm,A′B=BC+CA′=BC+AC=45cm,
cm,A′B=BC+CA′=BC+AC=45cm,∴AA′=
 =30
=30 cm.
cm.故选C.
点评:本题综合考查了勾股定理、含30°角的直角三角形以及旋转的性质.在直角三角形中,30度角所对的直角边等于斜边的一半,也是解决问题的关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 (2013•湖州二模)如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=25°,那么∠2的度数是( )
(2013•湖州二模)如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=25°,那么∠2的度数是( )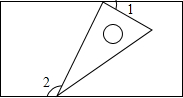 (2013•宜宾)如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2=
(2013•宜宾)如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2= 如图,一个含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到△A′B′C的位置,若BC的长为15cm,那么AA’的长为( )
如图,一个含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到△A′B′C的位置,若BC的长为15cm,那么AA’的长为( )
