题目内容
如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方位角为北偏东80°,测得C处的方位角为南偏东25°,航行1小时后到达C处,在C处测得A的方位角为北偏东20°,求C到A的距离.
【答案】分析:过点B作BD⊥AC于点D,根据三角函数分别求BD,AD的值,从而不难求AC的长.
解答: 解:过点B作BD⊥AC于点D.
解:过点B作BD⊥AC于点D.
∵△BCD是等腰直角三角形,
∴BD=CD=30× =15
=15 .
.
∵AD=BD•tan30°=5 ,
,
∴CA=15 +5
+5 =5(
=5( +3
+3 ).
).
故C到A的距离为5( +3
+3 )km.
)km.
点评:本题考查了解直角三角形的应用-方向角问题.解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
解答:
 解:过点B作BD⊥AC于点D.
解:过点B作BD⊥AC于点D.∵△BCD是等腰直角三角形,
∴BD=CD=30×
 =15
=15 .
.∵AD=BD•tan30°=5
 ,
,∴CA=15
 +5
+5 =5(
=5( +3
+3 ).
).故C到A的距离为5(
 +3
+3 )km.
)km.点评:本题考查了解直角三角形的应用-方向角问题.解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
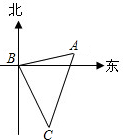 如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方位角为北偏东80°,测得C处的方位角为南偏东25°,航行1小时后到达C处,在C处测得A的方位角为北偏东20°,则C到A的距离是( )
如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方位角为北偏东80°,测得C处的方位角为南偏东25°,航行1小时后到达C处,在C处测得A的方位角为北偏东20°,则C到A的距离是( )A、15
| ||||
B、15
| ||||
C、15(
| ||||
D、5(
|
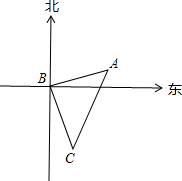 如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方位角为北偏东80°,测得C处的方位角为南偏东25°,航行1小时后到达C处,在C处测得A的方位角为北偏东20°,求C到A的距离.
如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方位角为北偏东80°,测得C处的方位角为南偏东25°,航行1小时后到达C处,在C处测得A的方位角为北偏东20°,求C到A的距离. 如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方位角为北偏东80°,测得C处的方位角为南偏东25°.航行1h后到达C处,在C处测得灯塔A的方位角为北偏东20°,则C到A的距离是
如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方位角为北偏东80°,测得C处的方位角为南偏东25°.航行1h后到达C处,在C处测得灯塔A的方位角为北偏东20°,则C到A的距离是 如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方位角为北偏东80°,测得C处的方位角为南偏东25°,航行1小时后到达C处,在C处测得A的方位角为北偏东20°,求C到A的距离.
如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方位角为北偏东80°,测得C处的方位角为南偏东25°,航行1小时后到达C处,在C处测得A的方位角为北偏东20°,求C到A的距离.
 km
km km
km +
+ )km
)km +3
+3 )km
)km