Question

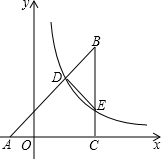（2013•宁波）如图，等腰直角三角形ABC顶点A在x轴上，∠BCA=90°，AC=BC=2

2

，反比例函数y=

3

x

（x＞0）的图象分别与AB，BC交于点D，E．连结DE，当△BDE∽△BCA时，点E的坐标为

（

3

2

2

，

2

）

．

Answer 1

分析：由相似三角形的对应角相等推知△BDE的等腰直角三角形；根据反比例函数图象上点的坐标特征可设E（a，

3

a

），D（b，

3

b

），由双曲线的对称性可以求得ab=3；最后，将其代入直线AD的解析式即可求得a的值．

解答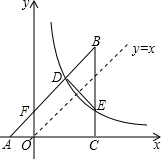：解：如图，∵∠BCA=90°，AC=BC=2

2

，反比例函数y=

3

x

（x＞0）的图象分别与AB，BC交于点D，E，
∴∠BAC=∠ABC=45°，且可设E（a，

3

a

），D（b，

3

b

），
∴C（a，0），B（a，2

2

），A（a-2

2

，0），
∴易求直线AB的解析式是：y=x+2

2

-a．
过点O作一，三象限的角平分线即直线y=x，
又∵△BDE∽△BCA，
∴∠BDE=∠BCA=90°，
∴直线y=x与直线DE垂直，
∴点D、E关于直线y=x对称，则

a+b

2

=

3 a + 3 b

2

，即ab=3．
又∵点D在直线AB上，
∴

3

b

=b+2

2

-a，即2a²-2

2

a-3=0，
解得，a=

3

2

2

，
∴点E的坐标是（

3

2

2

，

2

）．
故答案是：（

3

2

2

，

2

）．

点评：本题综合考查了相似三角形的性质、反比例函数图象上点的坐标特征、一次函数图象上的点的坐标特征、待定系数法求一次函数的解析式．解题时，注意双曲线的对称性的应用．