题目内容
 (2013•宁波)如图,梯形ABCD中,AD∥BC,AB=
(2013•宁波)如图,梯形ABCD中,AD∥BC,AB=| 5 |
| 2 |
分析:延长AE交BC于F,根据角平分线的定义可得∠BAF=∠DAF,再根据两直线平行,内错角相等可得∠DAF=∠AFB,然后求出∠BAF=∠AFB,再根据等角对等边求出AB=BF,然后求出FC,根据两组对边平行的四边形是平行四边形得到四边形AFCD是平行四边形,然后根据平行四边形的对边相等解答.
解答: 解:延长AE交BC于F,
解:延长AE交BC于F,
∵AE是∠BAD的平分线,
∴∠BAF=∠DAF,
∵AD∥CB,
∴∠DAF=∠AFB,
∴∠BAF=∠AFB,
∴AB=BF,
∵AB=
,BC=4,
∴CF=4-
=
,
∵AD∥BC,AE∥CD,
∴四边形AFCD是平行四边形,
∴AD=CF=
.
故选B.
 解:延长AE交BC于F,
解:延长AE交BC于F,∵AE是∠BAD的平分线,
∴∠BAF=∠DAF,
∵AD∥CB,
∴∠DAF=∠AFB,
∴∠BAF=∠AFB,
∴AB=BF,
∵AB=
| 5 |
| 2 |
∴CF=4-
| 5 |
| 2 |
| 3 |
| 2 |
∵AD∥BC,AE∥CD,
∴四边形AFCD是平行四边形,
∴AD=CF=
| 3 |
| 2 |
故选B.
点评:本题考查了梯形的性质,等腰三角形的性质,平行四边形的判定与性质,梯形的问题,关键在于准确作出辅助线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•宁波)如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
(2013•宁波)如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( ) (2013•宁波)如图,AE是半圆O的直径,弦AB=BC=4
(2013•宁波)如图,AE是半圆O的直径,弦AB=BC=4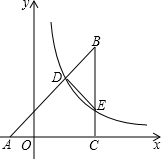 (2013•宁波)如图,等腰直角三角形ABC顶点A在x轴上,∠BCA=90°,AC=BC=2
(2013•宁波)如图,等腰直角三角形ABC顶点A在x轴上,∠BCA=90°,AC=BC=2