题目内容

P为正方形ABCD的对角线AC上任一点，若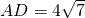 $数学公式$ ，则点P到AB、BC的距离之和为________．

$\text{[math]}$
分析：过点P作PE⊥AB于E，PF⊥BC于F，所以四边形EBFP是矩形，所以PF=BE，根据正方形的每一条对角线平分一组对角，∠BAC=45°，所以Rt△APE是等腰直角三角形，PE=AE，所以点P到AB、BC的距离之和等于正方形的边长．
解答：

解：如图，过点P作PE⊥AB于E，PF⊥BC于F，
则四边形EBFP是矩形，
∴PF=BE，
在正方形ABCD中，∠BAC=45°，
∴PE=AE，
∴PE+PF=BE+AE=AB=AD=4 $\text{[math]}$ ，
即点P到AB、BC的距离之和为4 $\text{[math]}$ ．
故答案为4 $\text{[math]}$ ．
点评：本题主要利用正方形的对角线平分一组对角的性质，把点P到AB、BC两边的距离之和转化为正方形的边长是解题的关键，也是本题的难点．

练习册系列答案

教材完全学案系列答案

精析巧练系列答案

今日课堂课时作业系列答案

金版卷王课程探究大试卷系列答案

金榜之路系列答案

金点中考系列答案

金海全A突破系列答案

金考卷45套汇编系列答案

全景文化中考试题汇编3年真题2年模拟系列答案

金牌教练赢在燕赵系列答案

相关题目

25、如图1，已知P为正方形ABCD的对角线AC上一点（不与A、C重合），PE⊥BC于点E，PF⊥CD于点F．
（1）求证：BP=DP；
（2）如图2，若四边形PECF绕点C按逆时针方向旋转，在旋转过程中是否总有BP=DP？若是，请给予证明；若不是，请用反例加以说明；
（3）试选取正方形ABCD的两个顶点，分别与四边形PECF的两个顶点连接，使得到的两条线段在四边形PECF绕点C按逆时针方向旋转的过程中长度始终相等，并证明你的结论．

26、如图1，O为正方形ABCD的中心，分别延长OA、OD到点F、E，使OF=2OA，OE=2OD，连接EF．将△EOF绕点O逆时针旋转α角得到△E₁OF₁（如图2）．
（1）探究AE₁与BF₁的数量关系，并给予证明；
（2）当α=30°时，求证：△AOE₁为直角三角形．

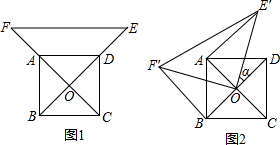（2013•四会市二模）如图1，已知O为正方形ABCD的中心，分别延长OA到点F，OD到点E，使OF=2OA，OE=2OD，连结EF，将△FOE绕点O逆时针旋转α角得到△F′OE′（如图2）．连结AE′、BF′．
（1）探究AE′与BF′的数量关系，
并给予证明；
（2）当α=30°，AB=2时，求：
①∠AE′O的度数；
②BF′的长度．

如图，点F为正方形ABCD的边CD的中点，E为BC上一点，M为EF上一点，且D、M关于AF对称，B、M关于AE对称，∠CFE的平分线交AE的延长线于G，交BC于N，连CG，下列结论：①△AFG为等腰直角三角形；②CG=2

CN；③S_△CEF=S_△ABE，其中正确的有（　　）

已知，AC为正方形ABCD的对角线，E为AC上一点，且AB=AE，EF⊥AC交BC于F，求证：FB=EC．