题目内容
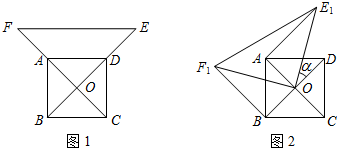
26、如图1,O为正方形ABCD的中心,分别延长OA、OD到点F、E,使OF=2OA,OE=2OD,连接EF.将△EOF绕点O逆时针旋转α角得到△E1OF1(如图2).
(1)探究AE1与BF1的数量关系,并给予证明;
(2)当α=30°时,求证:△AOE1为直角三角形.
(1)探究AE1与BF1的数量关系,并给予证明;
(2)当α=30°时,求证:△AOE1为直角三角形.

分析:(1)利用旋转不变量找到相等的角和线段,证得△E1AO≌△F1BO后即可证得结论;
(2)利用已知角,得出∠GAE1=∠GE 1A=30°,从而证明直角三角形.
(2)利用已知角,得出∠GAE1=∠GE 1A=30°,从而证明直角三角形.
解答:解:(1)AE1=BF1.
证明:∵O为正方形ABCD的中心,
∴OA=OD,
∵OF=2OA,OE=2OD,
∴OE=OF,
∵将△EOF绕点O逆时针旋转α角得到△E1OF1
∴OE1=OF1,
∵∠F1OB=∠E1OA,OA=OB,
∴△E1AO≌△F1BO,
∴AE1=BF1;
(2)∵取OE 1中点G,连接AG,
∵∠AOD=90°,α=30°,
∴∠E 1OA=90°-α=60°,
∵OE 1=2OA,∴OA=OG,
∴∠E 1OA=∠AGO═∠OAG=60°,
∴AG=GE 1,∴∠GAE1=∠GE 1A=30°,∴∠E1AO=90°,
∴△AOE1为直角三角形.
证明:∵O为正方形ABCD的中心,
∴OA=OD,
∵OF=2OA,OE=2OD,
∴OE=OF,
∵将△EOF绕点O逆时针旋转α角得到△E1OF1
∴OE1=OF1,
∵∠F1OB=∠E1OA,OA=OB,
∴△E1AO≌△F1BO,
∴AE1=BF1;
(2)∵取OE 1中点G,连接AG,
∵∠AOD=90°,α=30°,
∴∠E 1OA=90°-α=60°,
∵OE 1=2OA,∴OA=OG,

∴∠E 1OA=∠AGO═∠OAG=60°,
∴AG=GE 1,∴∠GAE1=∠GE 1A=30°,∴∠E1AO=90°,
∴△AOE1为直角三角形.
点评:本题考查了正方形的性质,利用正方形的特殊性质求解.结合了三角形全等的问题,并且涉及到探求性的问题,属于综合性比较强的问题.要求解此类问题就要对基本的知识点有很清楚的认识,熟练掌握.

练习册系列答案
相关题目
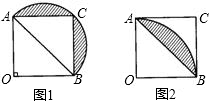 如图,四边形OBCA为正方形,图1是以AB为直径画半圆,阴影部分面积记为S1,图2是以O为圆心,OA长为半径画弧,阴影部分面积记为S2,则S1,S2的大小关系为( )
如图,四边形OBCA为正方形,图1是以AB为直径画半圆,阴影部分面积记为S1,图2是以O为圆心,OA长为半径画弧,阴影部分面积记为S2,则S1,S2的大小关系为( )| A、S1<S2 | B、S1=S2 | C、S1>S2 | D、无法判断 |

 (2013•泰安)如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=
(2013•泰安)如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=
