题目内容
 已知:如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且OA=AB=AD.
已知:如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且OA=AB=AD.
(1)求证:BD是⊙O的切线;
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且BE=8,tan∠BFA= ,求⊙O的半径长.
,求⊙O的半径长.
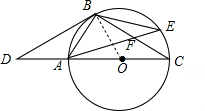 解:(1)如图:
解:(1)如图:连接OB,
∵OA=AB=OB,
∴△OAB是等边三角形,
∴∠OAB=∠OBA=60°,
∵AD=AB,
∴∠ABD=∠D=
 ∠OAB=30°.
∠OAB=30°.∴∠DBO=∠ABD+∠OBA=30°+60°=90°.
即OB⊥BD,
∴DB是⊙O的切线.
(2)∵AC是直径,点B在⊙O上,
∴∠ABC=90°,
∴△ABF为直角三角形,
在直角△ABF中,由tan∠BFA=
 ,设AB=
,设AB= a,则BF=2a,AF=3a,
a,则BF=2a,AF=3a,∴cos∠BFA=
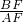 =
= =
= .
.∵∠C=∠E,∠AFC=∠BFE,
∴△AFC∽△BFE,
∴
 =
=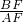 =
= ,
,∵BE=8,
∴AC=12.
因此圆的半径为6.
分析:(1)连接OB,得到△OAB是等边三角形,∠OBA=∠OAB=60°,再由AD=AB得到∠ABD=30°,所以∠DBO=90°,证明BD是⊙O的切线.
(2)在直角△ABF中,求出cos∠BFA的值,然后由△ACF∽△BEF,得到
 =
=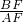 ,求出直径AC,再确定圆的半径的长.
,求出直径AC,再确定圆的半径的长.点评:本题考查的是切线的判定,(1)根据题目的条件求出∠DBO的度数,证明DB是圆的切线.(2)利用三角函数求出
 的值,然后利用相似三角形求出直径的长,再确定圆的半径的长.
的值,然后利用相似三角形求出直径的长,再确定圆的半径的长. 
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 BA.
BA.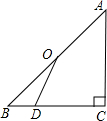 已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.
已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点. 10、已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( )
10、已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( ) B=∠DEB,EF⊥BC于点F,交⊙O于点M,EM=2
B=∠DEB,EF⊥BC于点F,交⊙O于点M,EM=2 25、已知:如图,点D是△ABC的边AC上的一点,过点D作DE⊥AB,DF⊥BC,E、F为垂足,再过点D作DG∥AB,交BC于点G,且DE=DF.
25、已知:如图,点D是△ABC的边AC上的一点,过点D作DE⊥AB,DF⊥BC,E、F为垂足,再过点D作DG∥AB,交BC于点G,且DE=DF.