题目内容
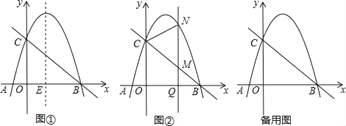
如图①已知抛物线y=ax2﹣3ax﹣4a（a＜0）的图象与x轴交于A、B两点（A在B的左侧），与y的正半轴交于点C，连结BC，二次函数的对称轴与x轴的交点为E．
（1）抛物线的对称轴与x轴的交点E坐标为_____，点A的坐标为_____；
（2）若以E为圆心的圆与y轴和直线BC都相切，试求出抛物线的解析式；
（3）在（2）的条件下，如图②Q（m，0）是x的正半轴上一点，过点Q作y轴的平行线，与直线BC交于点M，与抛物线交于点N，连结CN，将△CMN沿CN翻折，M的对应点为M′．在图②中探究：是否存在点Q，使得M′恰好落在y轴上？若存在，请求出Q的坐标；若不存在，请说明理由．
自1993年起，联合国将每年的3月22日定为“世界水日”，宗旨是唤起公众的节水意识，加强水资源保护．某校在开展“节约每一滴水”的活动中，从初三年级随机选出20名学生统计出各自家庭一个月的节约用水量，有关数据整理如下表．
节约用水量（单位：吨） | 1 | 1.2 | 1.4 | 2 | 2.5 |
家庭数 | 4 | 6 | 5 | 3 | 2 |
这组数据的中位数和众数分别是（ ）
A. 1.2，1.2； B. 1.4，1.2； C. 1.3，1.4； D. 1.3，1.2．
某商场同时购进甲、乙两种商品共200件，其进价和售价如下表，
商品名称 | 甲 | 乙 |
进价（元/件） | 80 | 100 |
售价（元/件） | 160 | 240 |
设其中甲种商品购进x件
（1）若该商场购进这200件商品恰好用去17900元，求购进甲、乙两种商品各多少件？
（2）若设该商场售完这200件商品的总利润为y元．
①求y与x的函数关系式；
②该商品计划最多投入18000元用于购买这两种商品，则至少要购进多少件甲商品？若售完这些商品，则商场可获得的最大利润是多少元？
（3）实际进货时，生产厂家对甲种商品的出厂价下调a元（50＜a＜70）出售，且限定商场最多购进120件，若商场保持同种商品的售价不变，请你根据以上信息及（2）中的条件，设计出使该商场获得最大利润的进货方案．
