Question

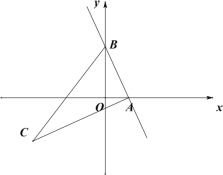
【题目】如图所示，已知直线与轴的正半轴交于点，与轴交于点，抛物线经过点与点，点在第三象限内，且，．

（1）当时，求抛物线的表达式；

（2）设点坐标为，试用分别表示；

（3）记，求的最大值．

Answer 1

【答案】（1）；（2）；（3）8

【解析】

（1）把A、B两点代入可求得结果；

（2）作CH⊥轴，构造直角三角形，根据找到已知边的关系，进而求得结果；

（3）由A、C两点可得到关于x、y的式子，代入计算即可．

解：（1）当时，,;

抛物线经过点与点;

∴所求抛物线的表达式为;

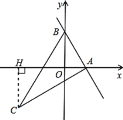
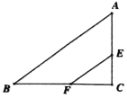
（2）如图：作CH⊥轴，垂足为点H，得∠AHC=∠AOB=90°;

∵AC⊥AB，

∴∠OAB+∠CAH=90°,

又∵∠CAH+∠ACH=90°，

∴∠OAB=∠ACH;

∴△AOB∽△CHA，

∴;

∵tan∠ABC=,

∴;

∵OA=，OB=2,

∴CH=2，AH=4;

∴点C的坐标为（4，2）．

∴.

（3）由点在轴的正半轴上，点C（4，2）在第三象限内得;

∴=();

∴当=2时取得最大值8．