题目内容
如图,黎叔叔想用60m长的篱笆靠墙MN围成一个矩形花圃ABCD,已知墙长MN=30m.
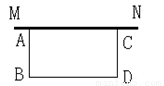
(1)能否使矩形花圃ABCD的面积为400m2?若能,请说明围法;若不能,请说明理由.
(2)请你帮助黎叔叔设计一种围法,使矩形花圃ABCD的面积最大,并求出最大面积.
【答案】
(1)能,长为20m,宽为20m;(2)长为30m,宽为15m时,面积最大为:450.
【解析】
试题分析:(1)由于篱笆总长为30m,设垂直于墙的AB边长为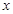 m,由此得到BD=(
m,由此得到BD=(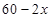 )m,接着根据题意列出方程
)m,接着根据题意列出方程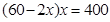 ,解方程即可求出AB的长;
,解方程即可求出AB的长;
(2)根据(1)得到矩形花圃ABCD的面积为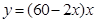 ,求出此函数的最值即可.
,求出此函数的最值即可.
试题解析:(1)依题意可知:AB边长为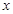 m,由此得到BD=(
m,由此得到BD=(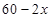 )m,∴
)m,∴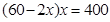 ,解得:
,解得: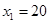 ,
,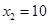 .当
.当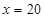 时,BD=
时,BD=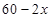 =20,当
=20,当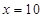 时,BD=
时,BD=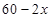 =40>30,∵墙可利用的最大长度为15m,∴
=40>30,∵墙可利用的最大长度为15m,∴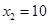 舍去.∴AB的长为20m,BD的长为20m;
舍去.∴AB的长为20m,BD的长为20m;
(2)设AB边长为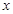 m,花圃的面积为
m,花圃的面积为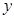 ,则
,则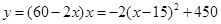 .
.
∴当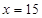 时,
时,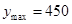 .而当
.而当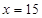 时,BD=
时,BD=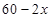 =30,可以构成矩形.
=30,可以构成矩形.
∴当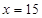 时,BD=
时,BD=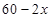 =30,可以构成的矩形的面积最大,为450
=30,可以构成的矩形的面积最大,为450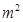 .
.
考点:1.一元二次方程的应用;2.二次函数的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图,小明想用皮尺测最池塘A、B间的距离,但现有皮尺无法直接测量,学习数学有关知识后,他想出了一个主意:先在地上取一个可以直接到达A、B两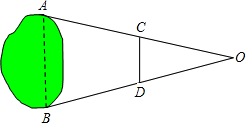 点的点O,连接OA、OB,分别在OA、OB上取中点C、D,连接CD,并测得CD=a,由此他即知道A、B距离是( )
点的点O,连接OA、OB,分别在OA、OB上取中点C、D,连接CD,并测得CD=a,由此他即知道A、B距离是( )
 点的点O,连接OA、OB,分别在OA、OB上取中点C、D,连接CD,并测得CD=a,由此他即知道A、B距离是( )
点的点O,连接OA、OB,分别在OA、OB上取中点C、D,连接CD,并测得CD=a,由此他即知道A、B距离是( )A、
| ||
| B、2a | ||
| C、a | ||
| D、3a |
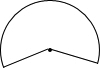 如图,小明想用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5cm,弧长是6πcm,那么围成的圆锥的高度是( )
如图,小明想用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5cm,弧长是6πcm,那么围成的圆锥的高度是( )A、
| ||
| B、5cm | ||
| C、4cm | ||
| D、3cm |
 如图,小明想用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5cm,弧长是6πcm,那么围成的圆锥的高度是
如图,小明想用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5cm,弧长是6πcm,那么围成的圆锥的高度是