题目内容
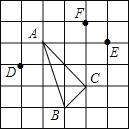
【题目】已知:如图1,在梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() ,
,![]() 上,
上,![]() =
=![]() =
=![]() .
.


(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 时,求证:四边形
时,求证:四边形![]() 是矩形;
是矩形;
(3)在(2)的条件下,如图2,过点![]() 作
作![]() 于点
于点![]() ,当
,当![]() ,
,![]() ,
,![]() 这三条线段的长度满足怎样的数量关系时,可以判断四边形
这三条线段的长度满足怎样的数量关系时,可以判断四边形![]() 是正方形?并说明理由.
是正方形?并说明理由.
【答案】(1)证明见详解;(2)证明见详解;(3) AD+BF=2GH,证明见详解.
【解析】
(1)要证明该四边形是平行四边形,只需证明 AE∥FG .根据对边对等角∠GFC =∠C,和等腰梯形的性质得到∠B = ∠C ,则∠B =∠GFC ,得到 AE∥FG .
(2)在平行四边形的基础上要证明是矩形,只需证明有一个角是直角.根据三角形 FGC 的内角和是 180 °,结合∠FGC = 2∠EFB和∠GFC =∠C ,得到∠BFE +GFC=90 °.则∠EFG = 90 °.
(3)题干要求![]() ,
,![]() ,
,![]() 这三条线段的长度数量关系并使得四边形
这三条线段的长度数量关系并使得四边形![]() 是正方形,根据题意作辅助线延长FB至点M,使BM=AD,连接EM,过点E作EN
是正方形,根据题意作辅助线延长FB至点M,使BM=AD,连接EM,过点E作EN![]() BF,垂足为N,得到
BF,垂足为N,得到![]() 继续分析求证即可.
继续分析求证即可.
解:证明:(1 ) ∵在梯形 ABCD 中,AB = DC ,∠ B = ∠ C ,
∵ GF = GC ,
∴∠ C = ∠ GFC ,∠ B = ∠ GFC,
∴ AB ∥ GF ,即 AE ∥ GF,
∵ AE = GF ,
∴四边形 AEFG 是平行四边形.
( 2 ) ∵∠ FGC + ∠ GFC + ∠ C = 180 o,∠ GFC = ∠ C ,∠ FGC = 2 ∠ EFB ,
∴ 2 ∠ GFC +2 ∠ EFB = 180 o,
∴∠ BFE + ∠ GFC = 90o.
∴∠ EFG = 90o.
∵四边形 AEFG 是平行四边形,
∴四边形 AEFG 是矩形.
(3)在(2)的条件下,当AD+BF=2GH时可以判断四边形AEFG是正方形.理由如下:
如图3,延长FB至点M,使BM=AD,连接EM,过点E作EN![]() BF,垂足为N,
BF,垂足为N,

则有MF=BM+BF=AD+BF=2GH,得到![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]() .
.
![]() ,
,
![]()
![]()
又![]()
![]()
![]() .
.
![]()
![]() .
.
![]() 四边形AEFG是矩形,
四边形AEFG是矩形,
![]() 四边形
四边形![]() 是正方形.
是正方形.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】第二十四届冬季奥林匹克运动会将与2022年2月20日在北京举行,北京将成为历史上第一座举办过夏奥会又举办过冬奥会的城市,东宝区举办了一次冬奥会知识网上答题竞赛,甲、乙两校各有400名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
(收集数据)
从甲、乙两校各随机抽取20名学生,在这次竞赛中它们的成绩如下:
甲 | 30 | 60 | 60 | 70 | 60 | 80 | 30 | 90 | 100 | 60 |
60 | 100 | 80 | 60 | 70 | 60 | 60 | 90 | 60 | 60 | |
乙 | 80 | 90 | 40 | 60 | 80 | 80 | 90 | 40 | 80 | 50 |
80 | 70 | 70 | 70 | 70 | 60 | 80 | 50 | 80 | 80 |
(整理、描述数据)按如下分数段整理、描述这两组样本数据:
(说明:优秀成绩为80<x≤100,良好成绩为50<x≤80,合格成绩为30≤x≤50.)
学校 | 平均分 | 中位数 | 众数 |
甲 | 67 | 60 | 60 |
乙 | 70 | 75 | a |
30≤x≤50 | 50<x≤80 | 80<x≤100 | |
甲 | 2 | 14 | 4 |
乙 | 4 | 14 | 2 |
(分析数据)两组样本数据的平均分、中位数、众数如右表所示:其中a= .
(得出结论)
(1)小伟同学说:“这次竞赛我得了70分,在我们学校排名属中游略偏上!”由表中数据可知小明是 校的学生;(填“甲”或“乙”)
(2)老师从乙校随机抽取一名学生的竞赛成绩,试估计这名学生的竞赛成绩为优秀的概率为 ;
(3)根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由.(至少从两个不同的角度说明推断的合理性)