题目内容
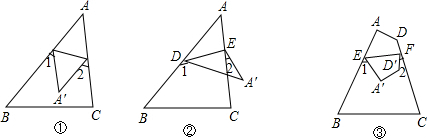
6.(1)如图①,把△ABC纸片沿DE折叠,当点A落在四边形BCED内部点A′的位置时,∠A、∠1、∠2之间有怎样的数量关系?并说明理由.(2)如图②,把△ABC纸片沿DE折叠,当点A落在四边形BCED外部点A′的位置时,∠A、∠1、∠2之间有怎样的数量关系?并说明理由.
(3)如图③,把四边形ABCD沿EF折叠,当点A、D分别落在四边形BCFE内部点A′、D′的位置时,你能求出∠A′、∠D′、∠1 与∠2之间的数量关系吗?并说明理由.
分析 (1)根据翻折的性质表示出∠3、∠4,再根据三角形的内角和定理列式整理即可得解;
(2)先根据翻折的性质以及平角的定义表示出∠3、∠4,再根据三角形的内角和定理列式整理即可得解;
(3)先根据翻折的性质表示出∠3、∠4,再根据四边形的内角和定理列式整理即可得解.
解答 解:(1)如图,根据翻折的性质,∠3=$\frac{1}{2}$(180-∠1),∠4=$\frac{1}{2}$(180-∠2),
∵∠A+∠3+∠4=180°,
∴∠A+$\frac{1}{2}$(180-∠1)+$\frac{1}{2}$(180-∠2)=180°,
整理得,2∠A=∠1+∠2;
(2)根据翻折的性质,∠3=$\frac{1}{2}$(180-∠1),∠4=$\frac{1}{2}$(180+∠2),
∵∠A+∠3+∠4=180°,
∴∠A+$\frac{1}{2}$(180-∠1)+$\frac{1}{2}$(180+∠2)=180°,
整理得,2∠A=∠1-∠2;
(3)根据翻折的性质,∠3=$\frac{1}{2}$(180-∠1),∠4=$\frac{1}{2}$(180-∠2),
∵∠A+∠D+∠3+∠4=360°,
∴∠A+∠D+$\frac{1}{2}$(180-∠1)+$\frac{1}{2}$(180-∠2)=360°,
整理得,2(∠A+∠D)=∠1+∠2+360°.
点评 本题主要考查了三角形的内角和定理,多边形的内角与外角,翻折的性质,整体思想的利用是解题的关键.

练习册系列答案
相关题目
16.如图的图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.一种面粉的质量标识为“25±0.25千克”,则下列面粉中合格的有( )
| A. | 25.51千克 | B. | 25.30千克 | C. | 24.80千克 | D. | 24.70千克 |
18.如果用+0.02克表示一只乒乓球质量超出标准质量0.02克,那么一只乒乓球质量低于标准质量0.02克记作( )
| A. | -0.02克 | B. | +0.02克 | C. | 0克 | D. | +0.04克 |
15.如图所反映的两个量中,其中y是x的函数的个数有( )


| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |