题目内容
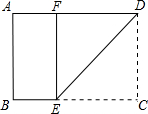
 如图,一张矩形纸片ABCD的长AD=8 cm,宽AB=4 cm,现将其折叠,使点D与点B重合,折痕为EF,则折痕EF的长是
如图,一张矩形纸片ABCD的长AD=8 cm,宽AB=4 cm,现将其折叠,使点D与点B重合,折痕为EF,则折痕EF的长是分析:本题可利用相似解决,由于折叠,可知BD⊥EF,利用直角三角形相似的性质:对应边成比例求得结果.
解答: 解:如图.
解:如图.
∵折叠,使点D与点B重合,
∴BD⊥EF,BO=DO
∵矩形ABCD,
∴∠C=90°,BD=
=
=4
cm,BO=2
cm
∵BD⊥EF,
∴∠BOF=∠C=90°,又∠CBD=∠OBF,
∴△BOF∽△BCD,
∴
=
,即
=
,
∴OF=
cm,
∴EF=2
cm.
 解:如图.
解:如图.∵折叠,使点D与点B重合,
∴BD⊥EF,BO=DO
∵矩形ABCD,
∴∠C=90°,BD=
| BC2+CD 2 |
| 82+42 |
| 5 |
| 5 |
∵BD⊥EF,
∴∠BOF=∠C=90°,又∠CBD=∠OBF,
∴△BOF∽△BCD,
∴
| BO |
| BC |
| OF |
| CD |
2
| ||
| 8 |
| OF |
| 4 |
∴OF=
| 5 |
∴EF=2
| 5 |
点评:折叠问题要要找清对应关系,重合的部分,重合的边,重合的角.这些关系在思考,做题时很有帮助.

练习册系列答案
相关题目
 如图是一张矩形纸片ABCD,AD=6cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=2cm,则DE=( )
如图是一张矩形纸片ABCD,AD=6cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=2cm,则DE=( )A、2
| ||
| B、4cm | ||
C、4
| ||
| D、6cm |
 3、如图是一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=6cm,则CD=( )
3、如图是一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=6cm,则CD=( ) 如图,一张矩形纸片沿BC折叠,顶点A落在点A′处,第二次过A′,再折叠,使折痕DE∥BC,若AB=2,AC=3,则梯形BDEC的面积为
如图,一张矩形纸片沿BC折叠,顶点A落在点A′处,第二次过A′,再折叠,使折痕DE∥BC,若AB=2,AC=3,则梯形BDEC的面积为 (2012•高淳县一模)如图,一张矩形纸片ABCD中,AD>AB.将矩形纸片ABCD沿过点A的直线折叠,使点D落到BC边上的点D′,折痕AE交DC于点E.
(2012•高淳县一模)如图,一张矩形纸片ABCD中,AD>AB.将矩形纸片ABCD沿过点A的直线折叠,使点D落到BC边上的点D′,折痕AE交DC于点E.