题目内容
如图8-1,在正方形ABCD和正方形BEFG中,点A,B,E在同一条直线上,连接DF,且P是线段DF的中点,连接PG,PC.
(1)如图8-1中,PG与PC的位置关系是 ,数量关系是 ;(2分)
(2) 如图8-2将条件“正方形ABCD和正方形BEFG”改为“矩形ABCD和矩形BEFG”其它条件不变,求证:PG=PC;(3分)

(3)如图8-3,若将条件“正方形ABCD和正方形BEFG”改为“菱形ABCD和菱形BEFG”,点A,B,E在同一条直线上,连接DF,P是线段DF的中点,连接PG、PC,且∠ABC=∠BEF=60°,求 的值
的值
(1) ,
, ;
;
(2)证明:延长GP交CD于H,∵P是DF的中点, ∴DP=FP
 由题意得矩形ABCD和矩形BEFG,点A,B,E在同一条直线上
由题意得矩形ABCD和矩形BEFG,点A,B,E在同一条直线上
∴DC∥GF∴∠HDP=∠GFP
又∵∠HPD=∠GPF
∴△DPH≌△FPG (ASA)
∴HP=GP
又∵∠HCG=90º,∴Rt△HCG中,P为HG的中点
∴PC= 即:PG=PC
即:PG=PC
(3)解:延长GP交CD于H, ∵P是DF的中点, ∴DP=FP
由题意在菱形ABCD和菱形BEFG,点A,B,E在同一条直线上
∴DC∥GF ∴∠HDP=∠GFP
又∵∠HPD=∠GPF ∴△DPH≌△FPG (ASA)
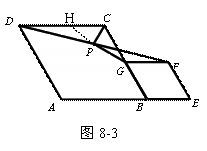 ∴HP=GP DH=FG
∴HP=GP DH=FG
又∵CD=CB,FG=GB ∴CD-DH=CB-FG即:CH=CG
∴△HCG是等腰三角形,
∴PC⊥PG ∠HCP=∠GCP (等腰三角形三线合一)
又∵∠ABC=60º∴∠GCP = ∠DCB= 60º
∠DCB= 60º
∴Rt△CPG中 
(其他证明方法和解法参考给分)

 锥后剩下的这个几何体的表面积.
锥后剩下的这个几何体的表面积.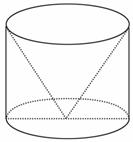
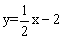 与x轴、y 轴分别交于点A 和点B ,点C在直线AB上,且点C 的纵坐标为一1 ,点D 在反比例函数
与x轴、y 轴分别交于点A 和点B ,点C在直线AB上,且点C 的纵坐标为一1 ,点D 在反比例函数
 的图象上 ,CD平行于y轴,
的图象上 ,CD平行于y轴,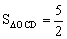 则k的值为 。
则k的值为 。
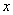 千米/小时,依据题意列方程正确的是( )
千米/小时,依据题意列方程正确的是( ) B.
B. C.
C.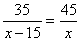
 D.
D.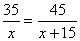

 的解集是 x > 2 ,则m的取值范围是 ( )
的解集是 x > 2 ,则m的取值范围是 ( )

