题目内容
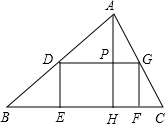
如图,E是矩形ABCD边BC的中点,P是AD边上一动点,PF⊥AE,PH⊥DE,垂足分别为F,H.
(1)当矩形ABCD的长与宽满足什么条件时,四边形PHEF是矩形?请予以证明;
(2)在(1)中,动点P运动到什么位置时,矩形PHEF变为正方形?为什么?

解:(1)AD=2AB.
证明:∵四边形ABCD是矩形,
∴AD=BC,AB=CD;
∵E是BC的中点,
∴AB=BE=EC=CD;
则△ABE、△DCE是等腰Rt△;
∴∠AEB=∠DEC=45°;
∴∠AED=90°;
四边形PFEH中,∠PFE=∠FEH=∠EHP=90°,故四边形PFEH是矩形;
(2)点P是AD的中点时,矩形PHEF变为正方形;理由如下:
由(1)可得∠BAE=∠CDE=45°;
∴∠FAP=∠HDP=45°;
又∵∠AFP=∠PHD=90°,AP=PD,
∴Rt△AFP≌Rt△DHP;
∴PF=PH;
在矩形PFEH中,PF=PH,故PFEH是正方形.
分析:(1)当四边形PFEH是矩形时,∠FEH=90°;易证得△ABE≌△DCE,则∠AEB=∠DEC=45°;那么△ABE、△DCE是等腰直角三角形,此时AB=BE=EC=CD,故矩形ABCD满足长是宽的2倍时,四边形PFEH是矩形;
(2)若矩形PHEF是正方形,则PF=PH,此时可证得△PAF≌△PDH,则AP=PD,所以当P为AD中点时,矩形PHEF变为正方形.
点评:此题主要考查了矩形、等腰直角三角形、全等三角形的判定和性质,以及正方形的判定.熟练掌握各特殊平行四边形的判定和性质是解答此题的关键.
证明:∵四边形ABCD是矩形,
∴AD=BC,AB=CD;
∵E是BC的中点,
∴AB=BE=EC=CD;
则△ABE、△DCE是等腰Rt△;
∴∠AEB=∠DEC=45°;
∴∠AED=90°;
四边形PFEH中,∠PFE=∠FEH=∠EHP=90°,故四边形PFEH是矩形;
(2)点P是AD的中点时,矩形PHEF变为正方形;理由如下:
由(1)可得∠BAE=∠CDE=45°;
∴∠FAP=∠HDP=45°;
又∵∠AFP=∠PHD=90°,AP=PD,
∴Rt△AFP≌Rt△DHP;
∴PF=PH;
在矩形PFEH中,PF=PH,故PFEH是正方形.
分析:(1)当四边形PFEH是矩形时,∠FEH=90°;易证得△ABE≌△DCE,则∠AEB=∠DEC=45°;那么△ABE、△DCE是等腰直角三角形,此时AB=BE=EC=CD,故矩形ABCD满足长是宽的2倍时,四边形PFEH是矩形;
(2)若矩形PHEF是正方形,则PF=PH,此时可证得△PAF≌△PDH,则AP=PD,所以当P为AD中点时,矩形PHEF变为正方形.
点评:此题主要考查了矩形、等腰直角三角形、全等三角形的判定和性质,以及正方形的判定.熟练掌握各特殊平行四边形的判定和性质是解答此题的关键.

练习册系列答案
相关题目

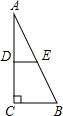 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )